目标
给你一棵以 root 为根的二叉树和一个 head 为第一个节点的链表。
如果在二叉树中,存在一条一直向下的路径,且每个点的数值恰好一一对应以 head 为首的链表中每个节点的值,那么请你返回 True ,否则返回 False 。
一直向下的路径的意思是:从树中某个节点开始,一直连续向下的路径。
示例 1:
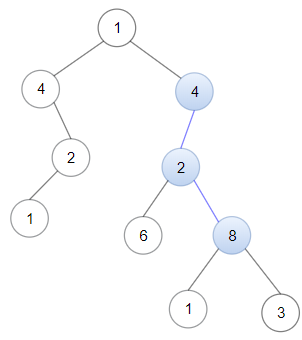
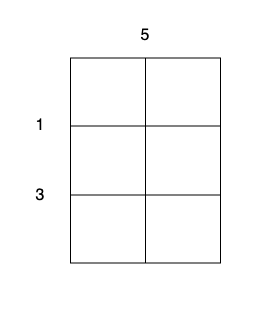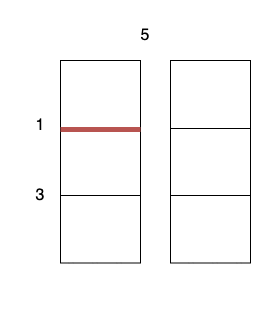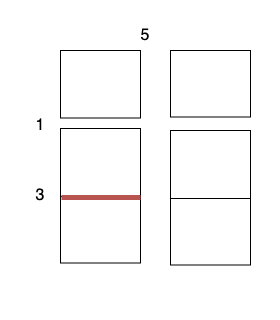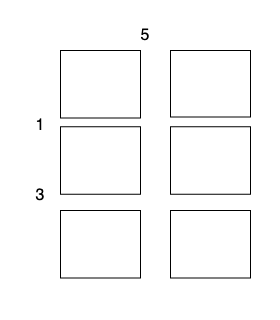
输入:head = [4,2,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
输出:true
解释:树中蓝色的节点构成了与链表对应的子路径。示例 2:
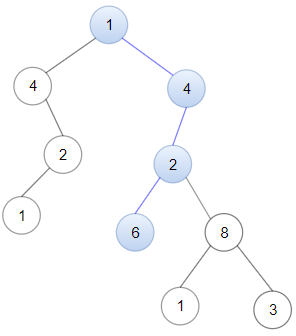
输入:head = [1,4,2,6], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
输出:true示例 3:
输入:head = [1,4,2,6,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
输出:false
解释:二叉树中不存在一一对应链表的路径。说明:
- 二叉树和链表中的每个节点的值都满足 1 <= node.val <= 100 。
- 链表包含的节点数目在 1 到 100 之间。
- 二叉树包含的节点数目在 1 到 2500 之间。
思路
判断二叉树中是否存在给定的路径 head,路径以链表的形式给出。
dfs 判断是否存在相同的路径。这道题的难点在于没有要求起点为 root,因此需要枚举所有节点为起点的情况。针对每一个起点我们最多检查 100 次,总共大概 2.5 * 10^5 次。
代码
/**
* @date 2024-12-30 8:56
*/
public class IsSubPath1367 {
public ListNode head;
public boolean isSubPath(ListNode head, TreeNode root) {
this.head = head;
return dfs(root, head);
}
public boolean dfs(TreeNode cur, ListNode node) {
if (node == null) {
return true;
}
if (cur == null) {
return false;
}
return cur.val == node.val && (dfs(cur.left, node.next) || dfs(cur.right, node.next))
|| node == head && (dfs(cur.left, head) || dfs(cur.right, head));
}
}
性能