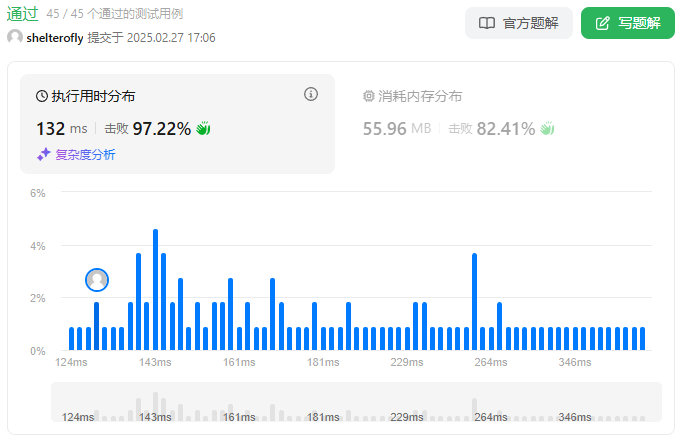
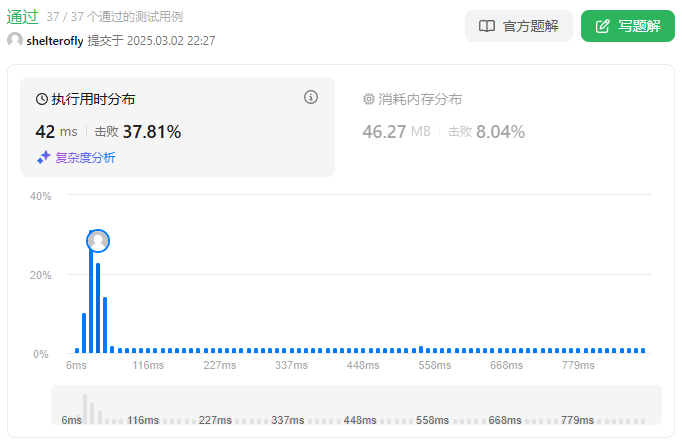
目标
请你设计一个带光标的文本编辑器,它可以实现以下功能:
- 添加:在光标所在处添加文本。
- 删除:在光标所在处删除文本(模拟键盘的删除键)。
- 移动:将光标往左或者往右移动。
当删除文本时,只有光标左边的字符会被删除。光标会留在文本内,也就是说任意时候 0 <= cursor.position <= currentText.length 都成立。
请你实现 TextEditor 类:
- TextEditor() 用空文本初始化对象。
- void addText(string text) 将 text 添加到光标所在位置。添加完后光标在 text 的右边。
- int deleteText(int k) 删除光标左边 k 个字符。返回实际删除的字符数目。
- string cursorLeft(int k) 将光标向左移动 k 次。返回移动后光标左边 min(10, len) 个字符,其中 len 是光标左边的字符数目。
- string cursorRight(int k) 将光标向右移动 k 次。返回移动后光标左边 min(10, len) 个字符,其中 len 是光标左边的字符数目。
示例 1:
输入:
["TextEditor", "addText", "deleteText", "addText", "cursorRight", "cursorLeft", "deleteText", "cursorLeft", "cursorRight"]
[[], ["leetcode"], [4], ["practice"], [3], [8], [10], [2], [6]]
输出:
[null, null, 4, null, "etpractice", "leet", 4, "", "practi"]
解释:
TextEditor textEditor = new TextEditor(); // 当前 text 为 "|" 。('|' 字符表示光标)
textEditor.addText("leetcode"); // 当前文本为 "leetcode|" 。
textEditor.deleteText(4); // 返回 4
// 当前文本为 "leet|" 。
// 删除了 4 个字符。
textEditor.addText("practice"); // 当前文本为 "leetpractice|" 。
textEditor.cursorRight(3); // 返回 "etpractice"
// 当前文本为 "leetpractice|".
// 光标无法移动到文本以外,所以无法移动。
// "etpractice" 是光标左边的 10 个字符。
textEditor.cursorLeft(8); // 返回 "leet"
// 当前文本为 "leet|practice" 。
// "leet" 是光标左边的 min(10, 4) = 4 个字符。
textEditor.deleteText(10); // 返回 4
// 当前文本为 "|practice" 。
// 只有 4 个字符被删除了。
textEditor.cursorLeft(2); // 返回 ""
// 当前文本为 "|practice" 。
// 光标无法移动到文本以外,所以无法移动。
// "" 是光标左边的 min(10, 0) = 0 个字符。
textEditor.cursorRight(6); // 返回 "practi"
// 当前文本为 "practi|ce" 。
// "practi" 是光标左边的 min(10, 6) = 6 个字符。
说明:
- 1 <= text.length, k <= 40
- text 只含有小写英文字母。
- 调用 addText ,deleteText ,cursorLeft 和 cursorRight 的 总 次数不超过 2 * 10^4 次。
进阶:你能设计并实现一个每次调用时间复杂度为 O(k) 的解决方案吗?
提示:
- Making changes in the middle of some data structures is generally harder than changing the front/back of the same data structure.
- Can you partition your data structure (text with cursor) into two parts, such that each part changes only near its ends?
- Can you think of a data structure that supports efficient removals/additions to the front/back?
- Try to solve the problem with two deques by maintaining the prefix and the suffix separately.
思路
设计一个文本编辑器,支持光标左右移动,在光标位置添加字符,删除光标左侧字符的功能。光标移动返回移动后,光标左侧的最多 10 个字符。删除字符返回实际删除的字符个数。
难点在于如何在 buffer 中间插入文本。
暴力解法就是将后面的字符平移,最坏的情况下,操作序列是add,左移,add,左移,……,那么总共移动的字符个数应该是 text.length * q * (q-1) / 2,q 是插入操作次数,插入最多 10^4,文本最大 40,大概 2 * 10^9,这样的复杂度竟然没有超时。
进阶的做法是使用对顶栈,使用两个栈,一个保存光标左侧字符,一个保存光标右侧字符。
prefix 0 ------> top | top <------ 0 suffix。光标左移就将左边的栈顶压到右边,右移反之。
StringBuilder 相关API:
- 使用 setLength 快速删除后缀
- 使用 charAt 移动单个字符
- 使用 substring 快速获取光标左边 10 个字符串
代码
/**
* @date 2025-02-27 8:41
*/
public class TextEditor {
StringBuilder prefix;
StringBuilder suffix;
public TextEditor() {
prefix = new StringBuilder();
suffix = new StringBuilder();
}
public void addText(String text) {
prefix.append(text);
}
public int deleteText(int k) {
int remainder = Math.max(0, prefix.length() - k);
int cnt = prefix.length() - remainder;
prefix.setLength(remainder);
return cnt;
}
public String cursorLeft(int k) {
while (k > 0 && prefix.length() > 0) {
suffix.append(prefix.charAt(prefix.length() - 1));
prefix.setLength(prefix.length() - 1);
k--;
}
return prefix.substring(Math.max(prefix.length() - 10, 0));
}
public String cursorRight(int k) {
while (k > 0 && suffix.length() > 0) {
prefix.append(suffix.charAt(suffix.length() - 1));
suffix.setLength(suffix.length() - 1);
k--;
}
return prefix.substring(Math.max(prefix.length() - 10, 0));
}
}
性能