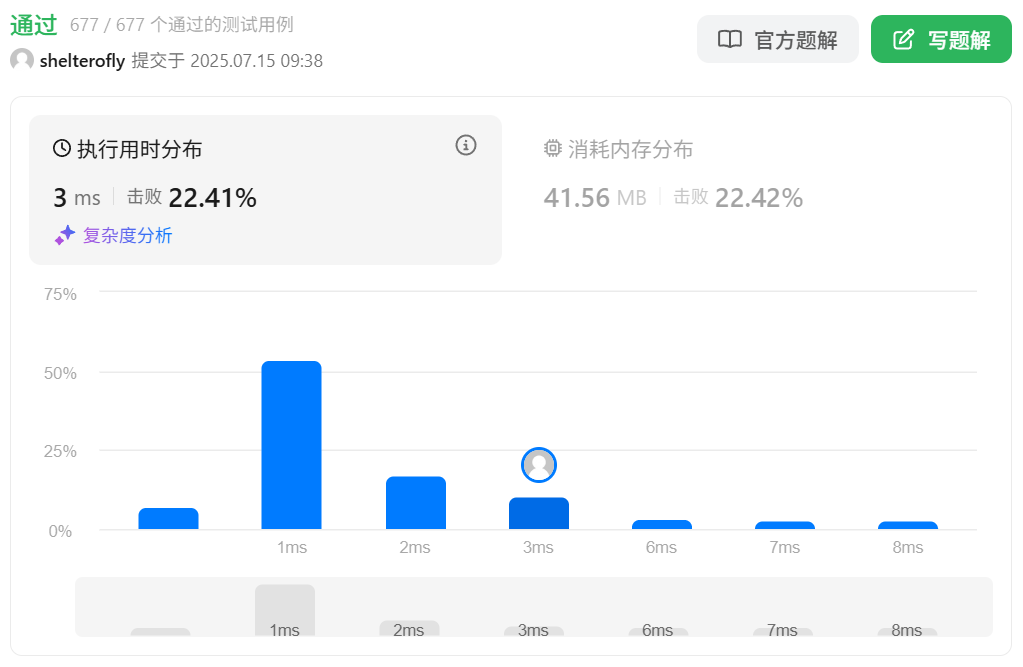
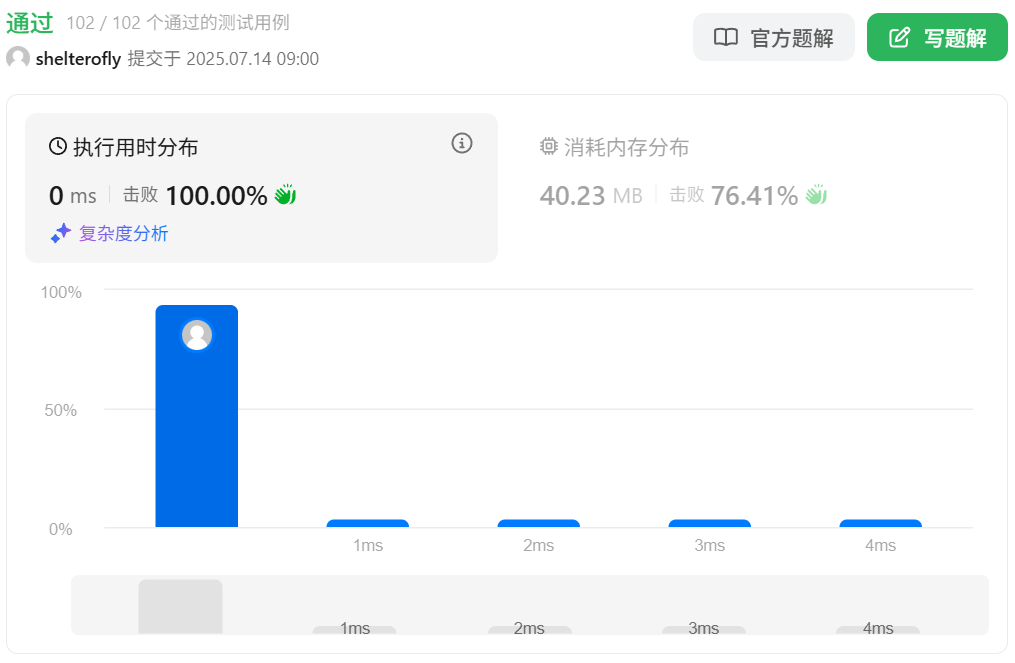
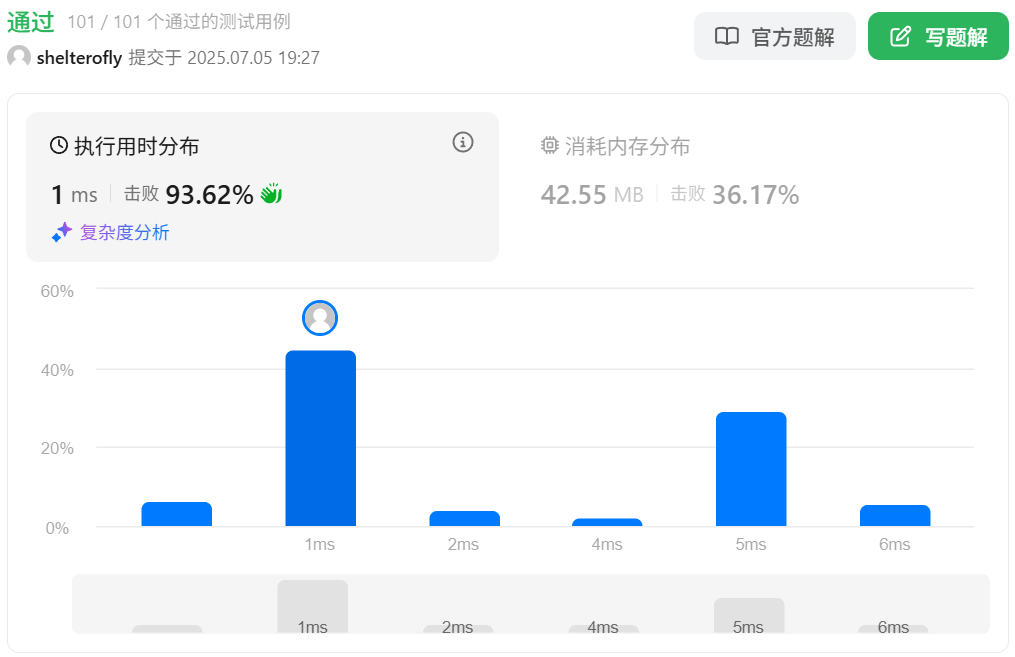
目标
有效单词 需要满足以下几个条件:
- 至少 包含 3 个字符。
- 由数字 0-9 和英文大小写字母组成。(不必包含所有这类字符。)
- 至少 包含一个 元音字母 。
- 至少 包含一个 辅音字母 。
给你一个字符串 word 。如果 word 是一个有效单词,则返回 true ,否则返回 false 。
注意:
- 'a'、'e'、'i'、'o'、'u' 及其大写形式都属于 元音字母 。
- 英文中的 辅音字母 是指那些除元音字母之外的字母。
示例 1:
输入:word = "234Adas"
输出:true
解释:
这个单词满足所有条件。示例 2:
输入:word = "b3"
输出:false
解释:
这个单词的长度少于 3 且没有包含元音字母。示例 3:
输入:word = "a3$e"
输出:false
解释:
这个单词包含了 '$' 字符且没有包含辅音字母。说明:
- 1 <= word.length <= 20
- word 由英文大写和小写字母、数字、'@'、'#' 和 '$' 组成。
思路
判断字符串是否至少包含 3 个字符,且仅由英文字母与数字组成,且至少包含一个元音字母和一个辅音字母。
正则表达式,前瞻断言。
代码
/**
* @date 2025-07-15 8:52
*/
public class IsValid3136 {
public static Pattern p = Pattern.compile("^(?=.*[aeiouAEIOU])(?=.*[b-df-hj-np-tv-zB-DF-HJ-NP-TV-Z])[0-9a-zA-z]{3,}$");
public boolean isValid(String word) {
return p.matcher(word).find();
}
}
性能