标签： easy

目标

超市正在促销，你可以用 numExchange 个空水瓶从超市兑换一瓶水。最开始，你一共购入了 numBottles 瓶水。

如果喝掉了水瓶中的水，那么水瓶就会变成空的。

给你两个整数 numBottles 和 numExchange ，返回你 最多 可以喝到多少瓶水。

示例 1：

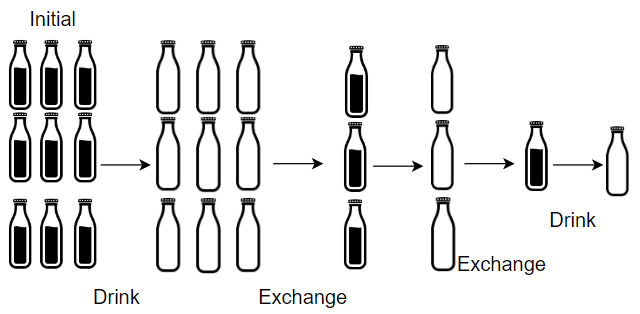
输入：numBottles = 9, numExchange = 3
输出：13
解释：你可以用 3 个空瓶兑换 1 瓶水。
所以最多能喝到 9 + 3 + 1 = 13 瓶水。

示例 2：

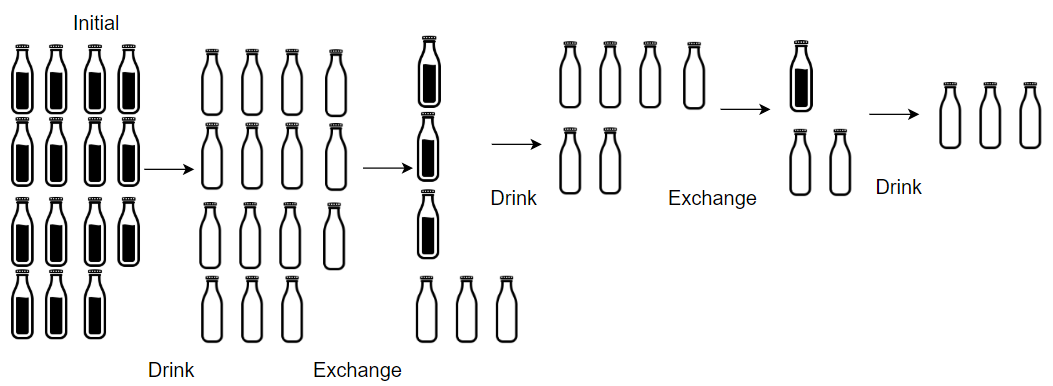
输入：numBottles = 15, numExchange = 4
输出：19
解释：你可以用 4 个空瓶兑换 1 瓶水。
所以最多能喝到 15 + 3 + 1 = 19 瓶水。

提示：

• 1 <= numBottles <= 100
• 2 <= numExchange <= 100

思路

有 numBottles 瓶水，numExchange 个空瓶可以兑换一瓶水，问最多可以喝几瓶水。

依题意模拟即可。空瓶数 = 剩余未兑换空瓶 + 新兑换瓶数。

代码

/**
 * @date 2025-10-01 19:05
 */
public class NumWaterBottles1518 {

    public int numWaterBottles(int numBottles, int numExchange) {
        int res = numBottles;
        while (numBottles >= numExchange) {
            int change = numBottles / numExchange;
            res += change;
            numBottles = numBottles % numExchange + change;
        }
        return res;
    }
}

性能

目标

给定由一些正数（代表长度）组成的数组 nums ，返回 由其中三个长度组成的、面积不为零的三角形的最大周长 。如果不能形成任何面积不为零的三角形，返回 0。

示例 1：

输入：nums = [2,1,2]
输出：5
解释：你可以用三个边长组成一个三角形:1 2 2。

示例 2：

输入：nums = [1,2,1,10]
输出：0
解释：
你不能用边长 1,1,2 来组成三角形。
不能用边长 1,1,10 来构成三角形。
不能用边长 1、2 和 10 来构成三角形。
因为我们不能用任何三条边长来构成一个非零面积的三角形，所以我们返回 0。

说明：

• 3 <= nums.length <= 10^4
• 1 <= nums[i] <= 10^6

思路

已知正整数数组 nums，从中取出三个元素作为三角形的边长，求三角形的最大周长。

最大周长一定是长度最长的三条边，只需要判断能否组成三角形即可。如果不能，说明当前最大值无法组成三角形，将其移除后按同样的逻辑继续判断即可。

代码

/**
 * @date 2025-09-28 8:50
 */
public class LargestPerimeter976 {

    public int largestPerimeter(int[] nums) {
        Arrays.sort(nums);
        int n = nums.length;
        for (int i = n - 1; i >= 2; i--) {
            if (nums[i] < nums[i - 1] + nums[i - 2]) {
                return nums[i] + nums[i - 1] + nums[i - 2];
            }
        }
        return 0;
    }

}

性能

目标

给你一个由 X-Y 平面上的点组成的数组 points ，其中 points[i] = [xi, yi] 。从其中取任意三个不同的点组成三角形，返回能组成的最大三角形的面积。与真实值误差在 10^-5 内的答案将会视为正确答案。

示例 1：

输入：points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
输出：2.00000
解释：输入中的 5 个点如上图所示，红色的三角形面积最大。

示例 2：

输入：points = [[1,0],[0,0],[0,1]]
输出：0.50000

提示：

• 3 <= points.length <= 50
• -50 <= xi, yi <= 50
• 给出的所有点 互不相同

思路

暴力解，三层循环，三角形面积可以使用向量的叉积计算。

向量的叉积表示这两个向量构成的平行四边形面积，除以 2 就是三角形的面积。

向量 (x1, y1) 与 (x2, y2) 的叉积等于 |x1 * y2 - x2 * y1|。

代码

/**
 * @date 2025-09-27 21:35
 */
public class LargestTriangleArea812 {

    public double largestTriangleArea(int[][] points) {
        int n = points.length;
        double res = 0.0;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                for (int k = j + 1; k < n; k++) {
                    int p1 = points[i][0];
                    int q1 = points[i][1];
                    int p2 = points[j][0];
                    int q2 = points[j][1];
                    int p3 = points[k][0];
                    int q3 = points[k][1];
                    res = Math.max(res, Math.abs((p2 - p1) * (q3 - q1) - (p3 - p1) * (q2 - q1)));
                }
            }
        }
        return res / 2;
    }
}

性能

目标

给你一个由 正整数 组成的数组 nums 。

返回数组 nums 中所有具有 最大 频率的元素的 总频率 。

元素的 频率 是指该元素在数组中出现的次数。

示例 1：

输入：nums = [1,2,2,3,1,4]
输出：4
解释：元素 1 和 2 的频率为 2 ，是数组中的最大频率。
因此具有最大频率的元素在数组中的数量是 4 。

示例 2：

输入：nums = [1,2,3,4,5]
输出：5
解释：数组中的所有元素的频率都为 1 ，是最大频率。
因此具有最大频率的元素在数组中的数量是 5 。

说明：

1 <= nums.length <= 100
1 <= nums[i] <= 100

思路

求正整数数组 nums 的最大频率之和。

针对元素计数，如果出现次数等于最大频率则累加最大频率，如果出现新的最大频率则需要将结果重置为最大频率。

代码

/**
 * @date 2025-09-22 8:48
 */
public class MaxFrequencyElements3005 {

    public int maxFrequencyElements_v1(int[] nums) {
        int res = 0;
        int[] cnt = new int[101];
        int max = 0;
        for (int num : nums) {
            cnt[num]++;
            if (max < cnt[num]) {
                max = cnt[num];
                res = cnt[num];
            } else if (max == cnt[num]) {
                res += cnt[num];
            }
        }
        return res;
    }

}

性能

目标

键盘出现了一些故障，有些字母键无法正常工作。而键盘上所有其他键都能够正常工作。

给你一个由若干单词组成的字符串 text ，单词间由单个空格组成（不含前导和尾随空格）；另有一个字符串 brokenLetters ，由所有已损坏的不同字母键组成，返回你可以使用此键盘完全输入的 text 中单词的数目。

示例 1：

输入：text = "hello world", brokenLetters = "ad"
输出：1
解释：无法输入 "world" ，因为字母键 'd' 已损坏。

示例 2：

输入：text = "leet code", brokenLetters = "lt"
输出：1
解释：无法输入 "leet" ，因为字母键 'l' 和 't' 已损坏。

示例 3：

输入：text = "leet code", brokenLetters = "e"
输出：0
解释：无法输入任何单词，因为字母键 'e' 已损坏。

说明：

• 1 <= text.length <= 10^4
• 0 <= brokenLetters.length <= 26
• text 由若干用单个空格分隔的单词组成，且不含任何前导和尾随空格
• 每个单词仅由小写英文字母组成
• brokenLetters 由 互不相同 的小写英文字母组成

思路

有一个字符串，其中的单词由空格分隔，现在键盘有一些按键不能正常工作，返回能够正常输入的单词个数。

使用哈希表记录不正常的按键，分割单词，判断单词是否包含不正常字符。

代码

/**
 * @date 2025-09-15 8:46
 */
public class CanBeTypedWords1935 {

    public int canBeTypedWords(String text, String brokenLetters) {
        Set<Character> brokenSet = new HashSet<>();
        for (char c : brokenLetters.toCharArray()) {
            brokenSet.add(c);
        }
        String[] words = text.split(" ");
        int res = words.length;
        for (String word : words) {
            for (char c : word.toCharArray()) {
                if (brokenSet.contains(c)){
                    res--;
                    break;
                }
            }
        }
        return res;
    }
}

性能

目标

给你一个由小写英文字母（'a' 到 'z'）组成的字符串 s。你的任务是找出出现频率 最高 的元音（'a'、'e'、'i'、'o'、'u' 中的一个）和出现频率最高的辅音（除元音以外的所有字母），并返回这两个频率之和。

注意：如果有多个元音或辅音具有相同的最高频率，可以任选其中一个。如果字符串中没有元音或没有辅音，则其频率视为 0。

一个字母 x 的 频率 是它在字符串中出现的次数。

示例 1：

输入: s = "successes"
输出: 6
解释:
元音有：'u' 出现 1 次，'e' 出现 2 次。最大元音频率 = 2。
辅音有：'s' 出现 4 次，'c' 出现 2 次。最大辅音频率 = 4。
输出为 2 + 4 = 6。

示例 2：

输入: s = "aeiaeia"
输出: 3
解释:
元音有：'a' 出现 3 次，'e' 出现 2 次，'i' 出现 2 次。最大元音频率 = 3。
s 中没有辅音。因此，最大辅音频率 = 0。
输出为 3 + 0 = 3。

说明:

• 1 <= s.length <= 100
• s 只包含小写英文字母

思路

计算字符串中辅音字母与元音字母的最高频率之和。

代码

/**
 * @date 2025-09-13 22:46
 */
public class MaxFreqSum3541 {

    public int maxFreqSum(String s) {
        int[] cnt = new int[26];
        int max = Integer.MIN_VALUE;
        int min = Integer.MAX_VALUE;
        for (char c : s.toCharArray()) {
            int i = c - 'a';
            if (c == 'a' || c == 'e' || c == 'i' || c == 'o' || c == 'u') {
                cnt[i]--;
                min = Math.min(min, cnt[i]);
            } else {
                cnt[i]++;
                max = Math.max(max, cnt[i]);
            }
        }
        return Math.max(0, max) - Math.min(0, min);
    }
}

性能

目标

给你一个下标从 0 开始的字符串 s ，将 s 中的元素重新 排列 得到新的字符串 t ，它满足：

• 所有辅音字母都在原来的位置上。更正式的，如果满足 0 <= i < s.length 的下标 i 处的 s[i] 是个辅音字母，那么 t[i] = s[i] 。
• 元音字母都必须以他们的 ASCII 值按 非递减 顺序排列。更正式的，对于满足 0 <= i < j < s.length 的下标 i 和 j ，如果 s[i] 和 s[j] 都是元音字母，那么 t[i] 的 ASCII 值不能大于 t[j] 的 ASCII 值。

请你返回结果字母串。

元音字母为 'a' ，'e' ，'i' ，'o' 和 'u' ，它们可能是小写字母也可能是大写字母，辅音字母是除了这 5 个字母以外的所有字母。

示例 1：

输入：s = "lEetcOde"
输出："lEOtcede"
解释：'E' ，'O' 和 'e' 是 s 中的元音字母，'l' ，'t' ，'c' 和 'd' 是所有的辅音。将元音字母按照 ASCII 值排序，辅音字母留在原地。

示例 2：

输入：s = "lYmpH"
输出："lYmpH"
解释：s 中没有元音字母（s 中都为辅音字母），所以我们返回 "lYmpH" 。

说明：

• 1 <= s.length <= 10^5
• s 只包含英语字母表中的 大写 和 小写 字母。

思路

有一个只包含英文字母的字符串，将其中的元音字母的位置按照 ASCII 码大小排序。

判断元音字母可以使用哈希表或者位运算。收集元音字母可以使用优先队列或者 StringBuilder 转成 charArray 之后再排序。

代码

/**
 * @date 2025-09-11 9:26
 */
public class SortVowels2785 {

    public static boolean[] isVowel = new boolean[26];

    static {
        isVowel[0] = true;
        isVowel['e' - 'a'] = true;
        isVowel['i' - 'a'] = true;
        isVowel['o' - 'a'] = true;
        isVowel['u' - 'a'] = true;
    }

    public String sortVowels(String s) {
        StringBuilder sb = new StringBuilder();
        char[] chars = s.toCharArray();
        for (char c : chars) {
            if (isVowel[Character.toLowerCase(c) - 'a']) {
                sb.append(c);
            }
        }
        char[] vowels = sb.toString().toCharArray();
        Arrays.sort(vowels);
        int j = 0;
        for (int i = 0; i < chars.length; i++) {
            if (isVowel[Character.toLowerCase(chars[i]) - 'a']) {
                chars[i] = vowels[j++];
            }
        }
        return new String(chars);
    }

}

性能

目标

「无零整数」是十进制表示中 不含任何 0 的正整数。

给你一个整数 n，请你返回一个 由两个整数组成的列表 [a, b]，满足：

• a 和 b 都是无零整数
• a + b = n

题目数据保证至少有一个有效的解决方案。

如果存在多个有效解决方案，你可以返回其中任意一个。

示例 1：

输入：n = 2
输出：[1,1]
解释：a = 1, b = 1。a + b = n 并且 a 和 b 的十进制表示形式都不包含任何 0。

示例 2：

输入：n = 11
输出：[2,9]

示例 3：

输入：n = 10000
输出：[1,9999]

示例 4：

输入：n = 69
输出：[1,68]

示例 5：

输入：n = 1010
输出：[11,999]

说明：

2 <= n <= 10^4

思路

有一个大于 1 的整数 n，将其转换成不包含 0 的整数 a 和 b，使得 a + b = n。

从低位到高位遍历，如果数字 d 大于 1，拆分为 1 和 d - 1，如果数字 d == 0 或 1 需要借位，拆分为 2 和 10 + d - 2。需要特别注意最高位是 1 的情况，直接将其加到其中一个数中即可。

代码

/**
 * @date 2025-09-08 8:50
 */
public class GetNoZeroIntegers1317 {

    public int[] getNoZeroIntegers(int n) {
        int a = 0, b = 0;
        int base = 1;
        while (n > 0) {
            int r = n % 10;
            n /= 10;
            if (r > 1) {
                a += base;
                b += (r - 1) * base;
            } else if (n == 0) {
                a += base;
            } else {
                r += 10;
                a += 2 * base;
                b += (r - 2) * base;
                n--;
            }
            base *= 10;
        }
        return new int[]{a, b};
    }

}

性能

目标

给你一个整数 n，请你返回 任意 一个由 n 个 各不相同 的整数组成的数组，并且这 n 个数相加和为 0 。

示例 1：

输入：n = 5
输出：[-7,-1,1,3,4]
解释：这些数组也是正确的 [-5,-1,1,2,3]，[-3,-1,2,-2,4]。

示例 2：

输入：n = 3
输出：[-1,0,1]

示例 3：

输入：n = 1
输出：[0]

说明：

• 1 <= n <= 1000

思路

构造 n 个不相同的数，使他们的和为 0。

一正一负，如果有剩余则为 0。

代码

/**
 * @date 2025-09-07 19:10
 */
public class SumZero1304 {

    public int[] sumZero(int n) {
        int[] res = new int[n];
        for (int i = 0; i < n - 1; i += 2) {
            res[i] = i + 1;
            res[i + 1] = -i - 1;
        }
        return res;
    }
}

性能

目标

给你三个整数 x、y 和 z，表示数轴上三个人的位置：

• x 是第 1 个人的位置。
• y 是第 2 个人的位置。
• z 是第 3 个人的位置，第 3 个人 不会移动 。

第 1 个人和第 2 个人以 相同 的速度向第 3 个人移动。

判断谁会 先 到达第 3 个人的位置：

• 如果第 1 个人先到达，返回 1 。
• 如果第 2 个人先到达，返回 2 。
• 如果两个人同时到达，返回 0 。

根据上述规则返回结果。

示例 1：

输入： x = 2, y = 7, z = 4
输出： 1
解释：
第 1 个人在位置 2，到达第 3 个人（位置 4）需要 2 步。
第 2 个人在位置 7，到达第 3 个人需要 3 步。
由于第 1 个人先到达，所以输出为 1。

示例 2：

输入： x = 2, y = 5, z = 6
输出： 2
解释：
第 1 个人在位置 2，到达第 3 个人（位置 6）需要 4 步。
第 2 个人在位置 5，到达第 3 个人需要 1 步。
由于第 2 个人先到达，所以输出为 2。

示例 3：

输入： x = 1, y = 5, z = 3
输出： 0
解释：
第 1 个人在位置 1，到达第 3 个人（位置 3）需要 2 步。
第 2 个人在位置 5，到达第 3 个人需要 2 步。
由于两个人同时到达，所以输出为 0。

说明：

1 <= x, y, z <= 100

思路

有三个数 x y z，判断 x 与 y 谁距离 z 最近，如果距离相同返回 0，x 更近返回 1，y 更近返回 2。

代码

/**
 * @date 2025-09-04 8:44
 */
public class FindClosest3516 {

    public int findClosest(int x, int y, int z) {
        int dx = Math.abs(x - z);
        int dy = Math.abs(y - z);
        return dx == dy ? 0 : dx < dy ? 1 : 2;
    }
}

性能