目标
给你一个整数数组 prices ,表示一支股票的历史每日股价,其中 prices[i] 是这支股票第 i 天的价格。
一个 平滑下降的阶段 定义为:对于 连续一天或者多天 ,每日股价都比 前一日股价恰好少 1 ,这个阶段第一天的股价没有限制。
请你返回 平滑下降阶段 的数目。
示例 1:
输入:prices = [3,2,1,4]
输出:7
解释:总共有 7 个平滑下降阶段:
[3], [2], [1], [4], [3,2], [2,1] 和 [3,2,1]
注意,仅一天按照定义也是平滑下降阶段。示例 2:
输入:prices = [8,6,7,7]
输出:4
解释:总共有 4 个连续平滑下降阶段:[8], [6], [7] 和 [7]
由于 8 - 6 ≠ 1 ,所以 [8,6] 不是平滑下降阶段。示例 3:
输入:prices = [1]
输出:1
解释:总共有 1 个平滑下降阶段:[1]说明:
- 1 <= prices.length <= 10^5
- 1 <= prices[i] <= 10^5
思路
求满足要求的子数组个数,要求子数组严格单调递减且相邻元素差为 1。
枚举右端点 r,假设满足条件的最小的左端点为 l,那么以 r 为右端点且满足条件的子数组个数为 r - l + 1。对于每一个 r,无需重复判断最小的 l,它可以从前一个状态转移过来,即如果 prices[r - 1] - prices[r] == 1 那么 l 仍是以 r - 1 为右端点且满足条件的最小左端点,否则 l = r。
代码
/**
* @date 2025-12-15 9:10
*/
public class GetDescentPeriods2110 {
public long getDescentPeriods(int[] prices) {
long res = 0L;
int l = 0;
int n = prices.length;
int prev = prices[0] + 1;
for (int r = 0; r < n; r++) {
if (prev - prices[r] != 1){
l = r;
}
res += r - l + 1;
prev = prices[r];
}
return res;
}
}
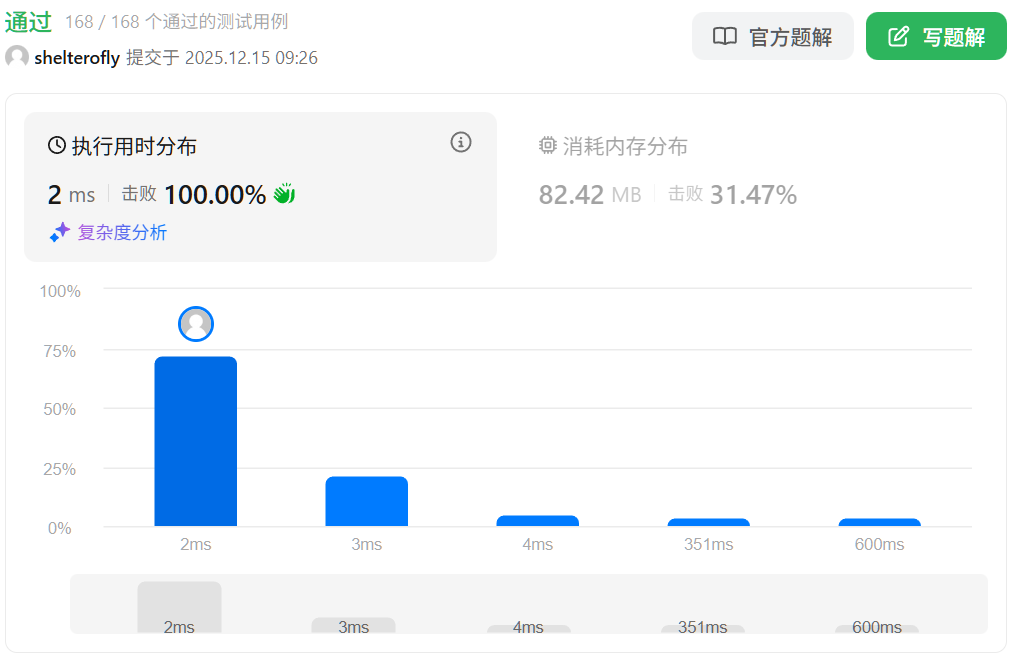
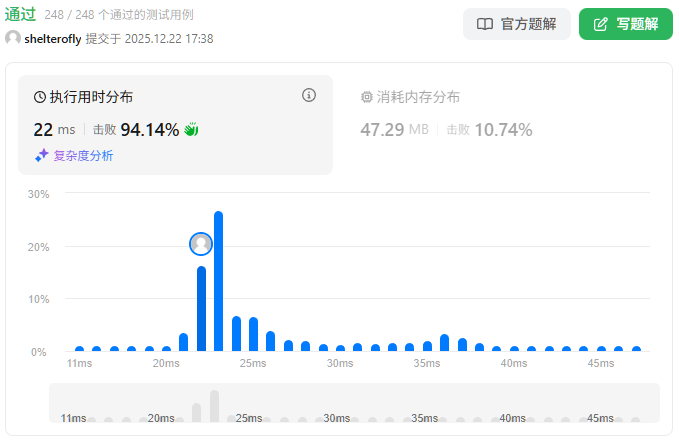
性能