分类： leetcode

目标

给你一个整数数组 nums ，如果 nums 至少 包含 2 个元素，你可以执行以下操作：

• 选择 nums 中的前两个元素并将它们删除。

一次操作的 分数 是被删除元素的和。

在确保 所有操作分数相同 的前提下，请你求出 最多 能进行多少次操作。

请你返回按照上述要求 最多 可以进行的操作次数。

示例 1：

输入：nums = [3,2,1,4,5]
输出：2
解释：我们执行以下操作：
- 删除前两个元素，分数为 3 + 2 = 5 ，nums = [1,4,5] 。
- 删除前两个元素，分数为 1 + 4 = 5 ，nums = [5] 。
由于只剩下 1 个元素，我们无法继续进行任何操作。

示例 2：

输入：nums = [3,2,6,1,4]
输出：1
解释：我们执行以下操作：
- 删除前两个元素，分数为 3 + 2 = 5 ，nums = [6,1,4] 。
由于下一次操作的分数与前一次不相等，我们无法继续进行任何操作。

说明：

• 2 <= nums.length <= 100
• 1 <= nums[i] <= 1000

思路

按照题目模拟即可。

代码

/**
 * @date 2024-06-07 0:00
 */
public class MaxOperations3038 {
    public int maxOperations(int[] nums) {
        int cnt = 1;
        int n = nums.length;
        int i = 2;
        int score = nums[0] + nums[1];
        while (i < n - 1) {
            int tmp = nums[i] + nums[i + 1];
            if (tmp == score) {
                i += 2;
                cnt++;
            } else {
                break;
            }
        }
        return cnt;
    }
}

性能

目标

Alice 有 n 枚糖，其中第 i 枚糖的类型为 candyType[i] 。Alice 注意到她的体重正在增长，所以前去拜访了一位医生。

医生建议 Alice 要少摄入糖分，只吃掉她所有糖的 n / 2 即可（n 是一个偶数）。Alice 非常喜欢这些糖，她想要在遵循医生建议的情况下，尽可能吃到最多不同种类的糖。

给你一个长度为 n 的整数数组 candyType ，返回： Alice 在仅吃掉 n / 2 枚糖的情况下，可以吃到糖的 最多 种类数。

示例 1：

输入：candyType = [1,1,2,2,3,3]
输出：3
解释：Alice 只能吃 6 / 2 = 3 枚糖，由于只有 3 种糖，她可以每种吃一枚。

示例 2：

输入：candyType = [1,1,2,3]
输出：2
解释：Alice 只能吃 4 / 2 = 2 枚糖，不管她选择吃的种类是 [1,2]、[1,3] 还是 [2,3]，她只能吃到两种不同类的糖。

示例 3：

输入：candyType = [6,6,6,6]
输出：1
解释：Alice 只能吃 4 / 2 = 2 枚糖，尽管她能吃 2 枚，但只能吃到 1 种糖。

说明：

• n == candyType.length
• 2 <= n <= 10^4
• n 是一个偶数
• -10^5 <= candyType[i] <= 10^5

思路

统计糖果种类，然后与n/2比较，取其中的最小值。

可以使用 HashSet 来计算种类数量，题解中最快的解法是自定义了hash函数，将种类映射到数组下标，通过判断相应位置上的值来计数。

代码

/**
 * @date 2024-06-02 9:26
 */
public class DistributeCandies575 {

    public int distributeCandies(int[] candyType) {
        int n = candyType.length;
        Set<Integer> set = new HashSet<>();
        for (int i = 0; i < n; i++) {
            set.add(candyType[i]);
        }
        return Math.min(set.size(), n / 2);
    }

    public int distributeCandies_v1(int[] candyType) {
        int res = 0;
        int n = candyType.length;
        byte[] mask = new byte[200001];
        for (int i = 0; i < n; i++) {
            int c = candyType[i];
            // 由于类型可能为负数，所以使用c+100000
            if (mask[c + 100000] == 0) {
                mask[c + 100000] = 1;
                res++;
                if (res > n / 2) return n / 2;
            }
        }
        return res;
    }
}

性能

目标

给你一个下标从 0 开始的二维整数矩阵 grid，大小为 n * n ，其中的值在 [1, n2] 范围内。除了 a 出现 两次，b 缺失 之外，每个整数都 恰好出现一次 。

任务是找出重复的数字a 和缺失的数字 b 。

返回一个下标从 0 开始、长度为 2 的整数数组 ans ，其中 ans[0] 等于 a ，ans[1] 等于 b 。

示例 1：

输入：grid = [[1,3],[2,2]]
输出：[2,4]
解释：数字 2 重复，数字 4 缺失，所以答案是 [2,4] 。

示例 2：

输入：grid = [[9,1,7],[8,9,2],[3,4,6]]
输出：[9,5]
解释：数字 9 重复，数字 5 缺失，所以答案是 [9,5] 。

说明：

• 2 <= n == grid.length == grid[i].length <= 50
• 1 <= grid[i][j] <= n * n
• 对于所有满足 1 <= x <= n * n 的 x ，恰好存在一个 x 与矩阵中的任何成员都不相等。
• 对于所有满足 1 <= x <= n * n 的 x ，恰好存在一个 x 与矩阵中的两个成员相等。
• 除上述的两个之外，对于所有满足 1 <= x <= n * n 的 x ，都恰好存在一对 i, j 满足 0 <= i, j <= n - 1 且 grid[i][j] == x 。

思路

记录元素的出现次数，选出其中出现次数为2和0的值即可。

网友还给出了一些位运算与数学公式求解的方法，可以降低空间复杂度，不用对每个元素计次，而是使用异或和与数学公式求解。

异或和求解的关键是如何区分得到的 a ^ b，由于a 与 b 不同，异或的结果至少有一个非0位，可以根据该bit位分组，这样每一组中就只含有a或b。

至于数学公式求解的关键是，通过各项和的差可以得到 b - a，各项平方和的差可以得到 b^2 - a^2，进而求得 b + a，解方程组可得a、b。

代码

/**
 * @date 2024-05-31 0:12
 */
public class FindMissingAndRepeatedValues2965 {

/**
     * 公式求和 1，2，……，n^2 以及 1^2，2^2，……，n^2
     * 然后遍历求和，二者之差为b - a 和 b^2 - a^2
     * 进而可以求得b + a，解方程可得a、b
     */
    public int[] findMissingAndRepeatedValues_v2(int[][] grid) {
        int n = grid.length;
        int n2 = n * n;
        long sum = 0;
        long sum2 = 0;
        for (int[] row : grid) {
            for (int i : row) {
                sum += i;
                sum2 += i * i;
            }
        }
        long bsuba = n2 * (n2 + 1L) / 2 - sum;
        long b2suba2 = n2 * (n2 + 1L) * (2 * n2 + 1) / 6 - sum2;
        long badda = b2suba2 / bsuba;
        long b = (badda + bsuba) / 2L;
        long a = badda - b;
        return new int[]{(int) a, (int) b};
    }

    /**
     * 异或和
     */
    public int[] findMissingAndRepeatedValues_v1(int[][] grid) {
        int n = grid.length;
        int n2 = n * n;
        int prefix = 0;
        for (int i = 1; i <= n2; i++) {
            prefix ^= i;
        }
        int tmp = 0;
        for (int[] row : grid) {
            for (int element : row) {
                tmp ^= element;
            }
        }
        int axorb = prefix ^ tmp;
        int shift = Integer.numberOfTrailingZeros(axorb);
        int[] res = new int[2];
        // 由于axorb至少有1bit是不同的，那么根据该bit分组，这样每一组里面a b是分开的
        for (int i = 1; i <= n2; i++) {
            res[i >> shift & 1] ^= i;
        }
        for (int[] row : grid) {
            for (int element : row) {
                res[element >> shift & 1] ^= element;
            }
        }
        // 由于顺序是不确定的，判断出现的为a
        for (int[] row : grid) {
            for (int element : row) {
                if (element == res[0]){
                    return res;
                }
            }
        }
        // 调换位置
        return new int[]{res[1], res[0]};
    }

    public int[] findMissingAndRepeatedValues(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int l = m * n + 1;
        int[] occurrence = new int[l];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                occurrence[grid[i][j]]++;
            }
        }
        int[] res = new int[2];
        for (int i = 1; i < l; i++) {
            if (occurrence[i] == 0) {
                res[1] = i;
            } else if (occurrence[i] == 2) {
                res[0] = i;
            }
        }
        return res;
    }
}

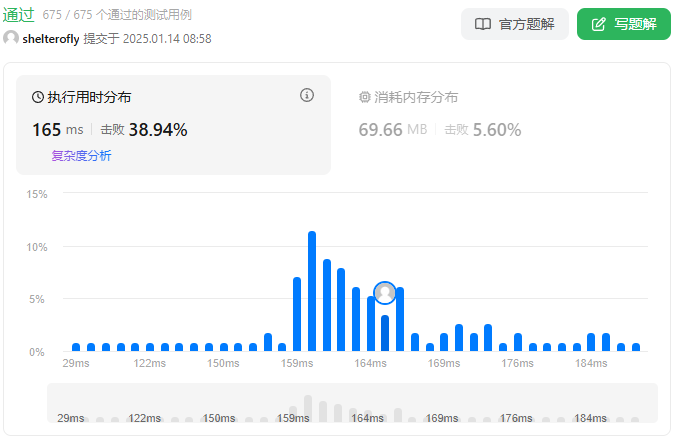
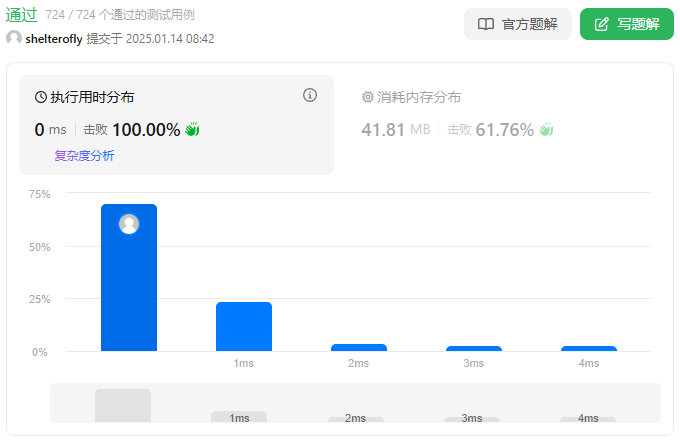
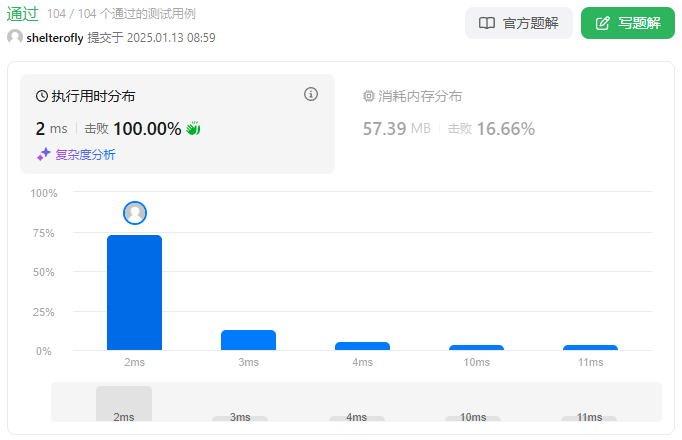
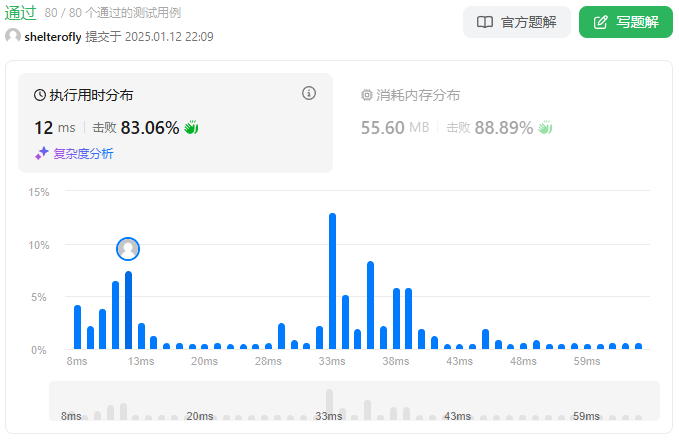
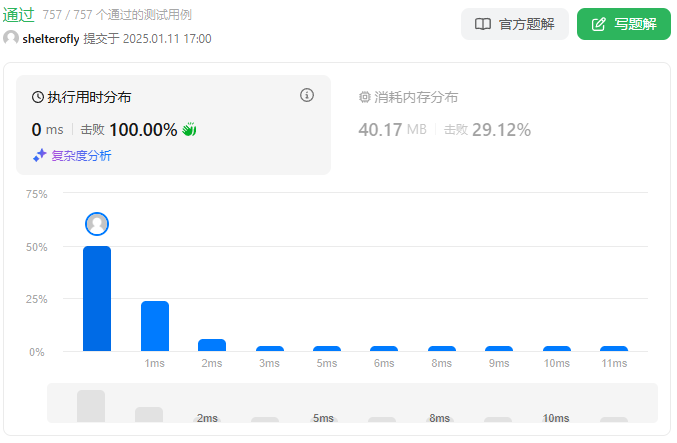
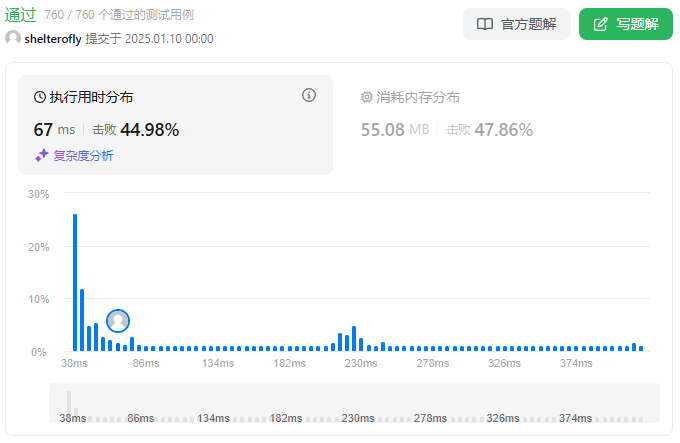
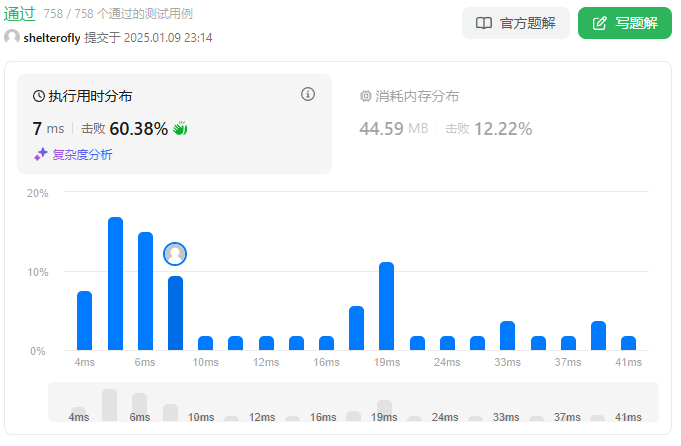
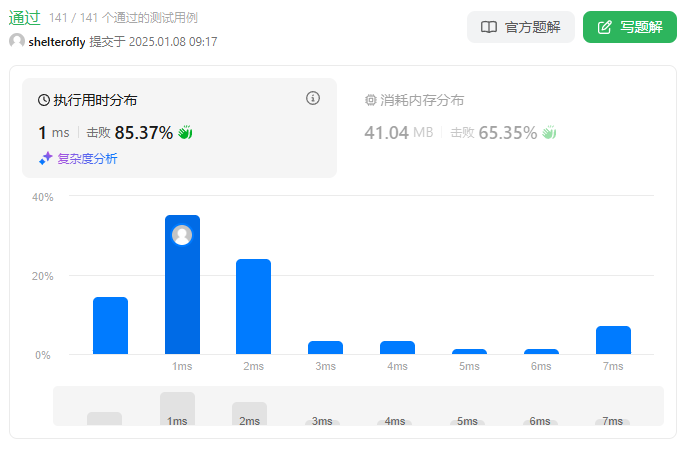
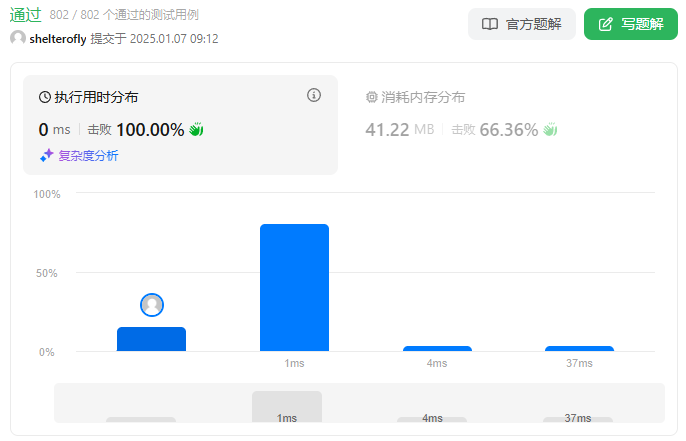
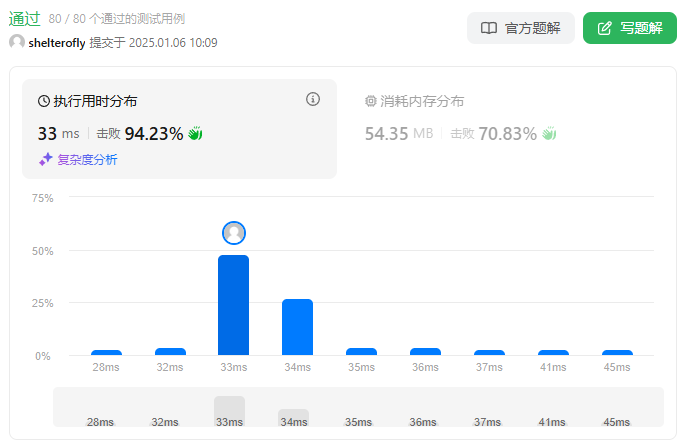
性能