目标
给你一个大小为 n x n 的整数矩阵 board ,方格按从 1 到 n2 编号,编号遵循 转行交替方式 ,从左下角开始 (即,从 board[n - 1][0] 开始)的每一行改变方向。
你一开始位于棋盘上的方格 1。每一回合,玩家需要从当前方格 curr 开始出发,按下述要求前进:
- 选定目标方格 next ,目标方格的编号在范围 [curr + 1, min(curr + 6, n2)] 。
- 该选择模拟了掷 六面体骰子 的情景,无论棋盘大小如何,玩家最多只能有 6 个目的地。
- 传送玩家:如果目标方格 next 处存在蛇或梯子,那么玩家会传送到蛇或梯子的目的地。否则,玩家传送到目标方格 next 。
- 当玩家到达编号 n2 的方格时,游戏结束。
如果 board[r][c] != -1 ,位于 r 行 c 列的棋盘格中可能存在 “蛇” 或 “梯子”。那个蛇或梯子的目的地将会是 board[r][c]。编号为 1 和 n2 的方格不是任何蛇或梯子的起点。
注意,玩家在每次掷骰的前进过程中最多只能爬过蛇或梯子一次:就算目的地是另一条蛇或梯子的起点,玩家也 不能 继续移动。
- 举个例子,假设棋盘是 [[-1,4],[-1,3]] ,第一次移动,玩家的目标方格是 2 。那么这个玩家将会顺着梯子到达方格 3 ,但 不能 顺着方格 3 上的梯子前往方格 4 。(简单来说,类似飞行棋,玩家掷出骰子点数后移动对应格数,遇到单向的路径(即梯子或蛇)可以直接跳到路径的终点,但如果多个路径首尾相连,也不能连续跳多个路径)
-1(4) 4(3)
-1(1) 3(2)返回达到编号为 n2 的方格所需的最少掷骰次数,如果不可能,则返回 -1。
示例 1:
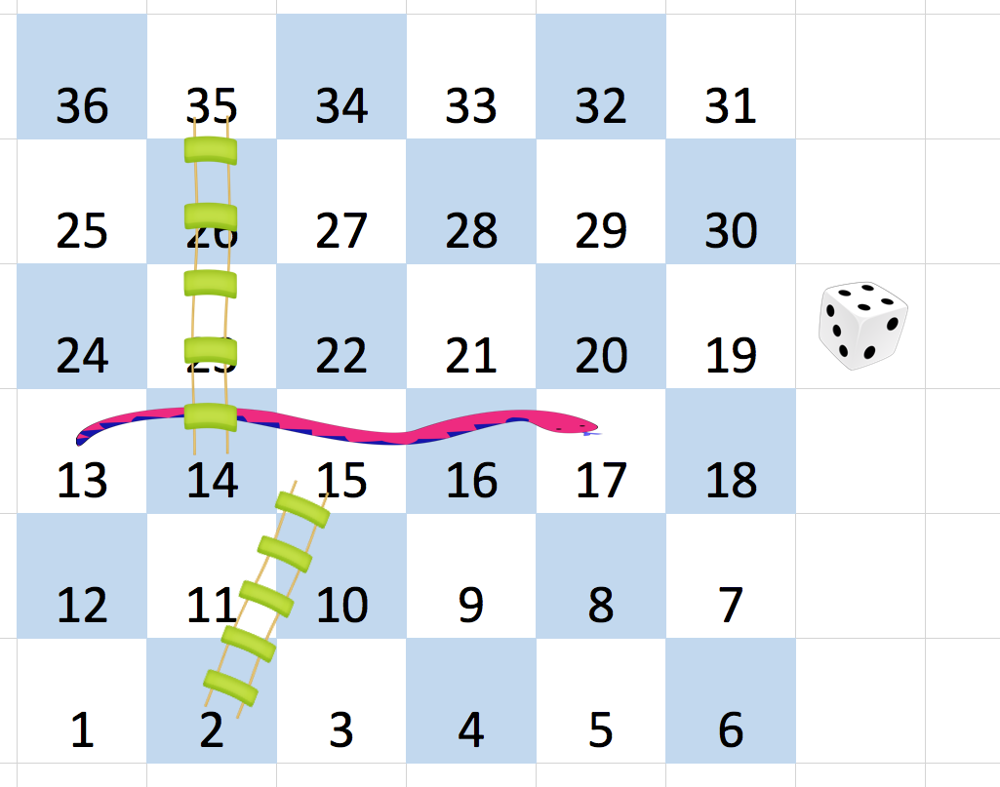
输入:board = [[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,35,-1,-1,13,-1],[-1,-1,-1,-1,-1,-1],[-1,15,-1,-1,-1,-1]]
输出:4
解释:
首先,从方格 1 [第 5 行,第 0 列] 开始。
先决定移动到方格 2 ,并必须爬过梯子移动到到方格 15 。
然后决定移动到方格 17 [第 3 行,第 4 列],必须爬过蛇到方格 13 。
接着决定移动到方格 14 ,且必须通过梯子移动到方格 35 。
最后决定移动到方格 36 , 游戏结束。
可以证明需要至少 4 次移动才能到达最后一个方格,所以答案是 4 。 示例 2:
输入:board = [[-1,-1],[-1,3]]
输出:1说明:
- n == board.length == board[i].length
- 2 <= n <= 20
board[i][j]的值是 -1 或在范围[1, n^2]内- 编号为 1 和 n^2 的方格上没有蛇或梯子
思路
有一个 n x n 棋盘 board,左下角从 1 开始编号,换行时改变编号顺序,例如 4 x 4 棋盘格子编号如下:
16 15 14 13
9 10 11 12
8 7 6 5
1 2 3 4玩家投骰子 1 ~ 6,根据点数移动到编号为 cur + point 的格子上,如果目标格子的值不为 -1,则传送到对应的格子编号。求到达终点所需的最小步数。
首先要解决棋盘编号与格子坐标的转换关系,然后使用 bfs 尝试所有可能的走法,并记录步数。为了防止到达不了终点陷入死循环,需要记录已经访问过的编号。
int row = m - 1 - (no - 1) / n;int col = (m - 1 - row) % 2 == 0 ? (no - 1) % n : n - 1 - (no - 1) % n;
代码
/**
* @date 2025-04-21 8:46
*/
public class SnakesAndLadders909 {
public int snakesAndLadders(int[][] board) {
int m = board.length;
int n = board[0].length;
int end = m * n;
int res = 0;
boolean[] visited = new boolean[end + 1];
Queue<Integer> q = new ArrayDeque<>();
q.add(1);
while (!q.isEmpty()) {
res++;
int size = q.size();
for (int i = 0; i < size; i++) {
Integer cur = q.poll();
for (int no = cur + 1; no <= cur + 6; no++) {
if (no == end) {
return res;
}
if (visited[no]) {
continue;
}
visited[no] = true;
int row = m - 1 - (no - 1) / n;
int col = (m - 1 - row) % 2 == 0 ? (no - 1) % n : n - 1 - (no - 1) % n;
if (board[row][col] == -1) {
q.offer(no);
} else {
if (board[row][col] == end) {
return res;
}
q.offer(board[row][col]);
}
}
}
}
return -1;
}
}
性能