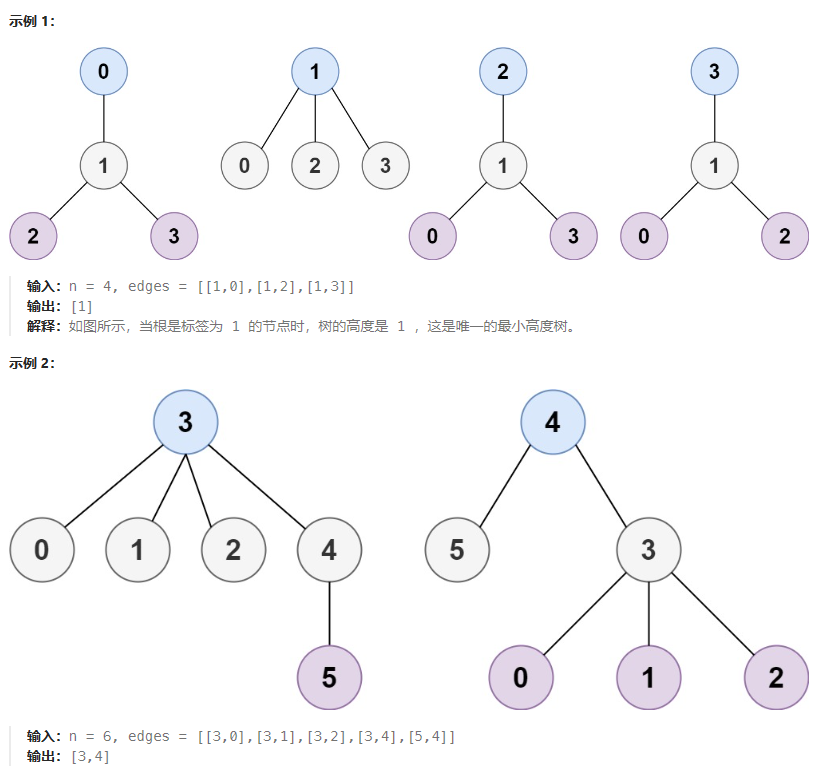
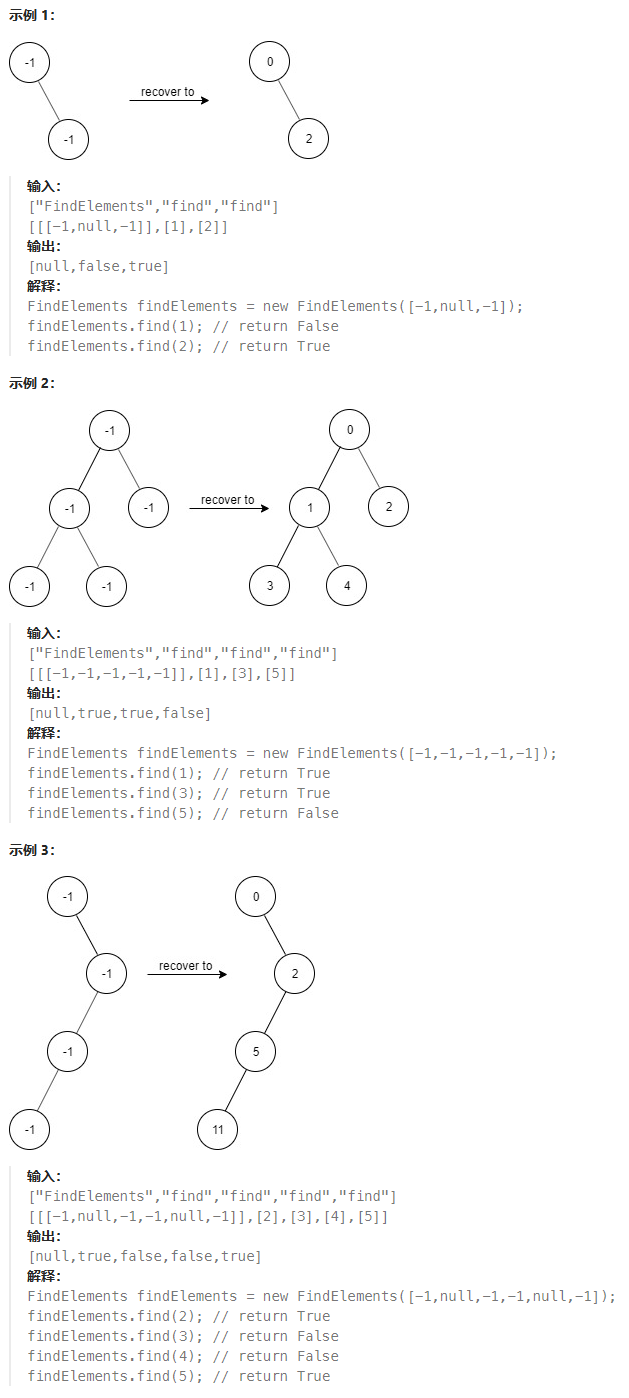
目标
你需要访问 n 个房间,房间从 0 到 n - 1 编号。同时,每一天都有一个日期编号,从 0 开始,依天数递增。你每天都会访问一个房间。
最开始的第 0 天,你访问 0 号房间。给你一个长度为 n 且 下标从 0 开始 的数组 nextVisit 。在接下来的几天中,你访问房间的 次序 将根据下面的 规则 决定:
- 假设某一天,你访问 i 号房间。
- 如果算上本次访问,访问 i 号房间的次数为 奇数 ,那么 第二天 需要访问 nextVisit[i] 所指定的房间,其中 0 <= nextVisit[i] <= i 。
- 如果算上本次访问,访问 i 号房间的次数为 偶数 ,那么 第二天 需要访问 (i + 1) mod n 号房间。
请返回你访问完所有房间的第一天的日期编号。题目数据保证总是存在这样的一天。由于答案可能很大,返回对 10^9 + 7 取余后的结果。
示例 1:
输入:nextVisit = [0,0]
输出:2
解释:
- 第 0 天,你访问房间 0 。访问 0 号房间的总次数为 1 ,次数为奇数。
下一天你需要访问房间的编号是 nextVisit[0] = 0
- 第 1 天,你访问房间 0 。访问 0 号房间的总次数为 2 ,次数为偶数。
下一天你需要访问房间的编号是 (0 + 1) mod 2 = 1
- 第 2 天,你访问房间 1 。这是你第一次完成访问所有房间的那天。示例 2:
输入:nextVisit = [0,0,2]
输出:6
解释:
你每天访问房间的次序是 [0,0,1,0,0,1,2,...] 。
第 6 天是你访问完所有房间的第一天。示例 3:
输入:nextVisit = [0,1,2,0]
输出:6
解释:
你每天访问房间的次序是 [0,0,1,1,2,2,3,...] 。
第 6 天是你访问完所有房间的第一天。说明:
- n == nextVisit.length
- 2 <= n <= 10^5
- 0 <= nextVisit[i] <= i
思路
这道题用了3.5小时,也不知道花费这么多精力到底值不值得。这道题基本上是调试出来的,好多坑都没有考虑到。
说回这道题,有 0 到 n-1 共 n 个房间,每天可以访问一个房间,第 0 天访问 0 号房,然后根据当前房间的被访问次数来决定明天访问的房间。通俗来讲就是,如果当前房间cur被访问次数为奇数,访问包括当前房间在内的由参数指定的房间[0, cur];如果为偶数,则访问编号为cur+1的房间。需要我们返回首次访问 n-1 房间是第几天。
我上来想都没想就直接按照题意把代码写出来了,主要是理解题意。不出所料,提交超时。
在第30个用例的时候超时了,参数是这样的 [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],即每前进一个房间都退回到第0个房间从头开始。总共 74 个房间,由于每个房间需要访问偶数次才可以前进,因此 f(n) = 2(f(n-1) + 1) 其中 f(0)=0, f(1)=2,n为正整数。两边都加上2得f(n) + 2 = 2(f(n-1) + 2),根据等比数列公式an = a1*q^(n-1),代入a1 = f(1) + 2 = 4, q = 2,得 f(n) = 2^(n+1) - 2。访问到编号为 74-1 的房间要等到第 2^74 -2 天。计算这个主要是为了说明问题的规模,按照题目描述去循环肯定是不行的。
很明显我们需要使用动态规划来求解。那么状态转移方程如何写?哪些子问题是重复计算的?经过观察我们知道,首次访问到某一房间的时候,之前所有房间的访问次数一定是偶数。当我们根据参数向后返回的时候,相当于是从指定的房间到当前房间又重新经历了一遍,因为参数指定的房间是固定的。于是我们可以保存首次访问到某房间是第几天,当后退到某房间之后就不用再重新循环了,直接计算天数,即天数累加上 dp[max] - dp[back] + 1。
上面的算法是题目完成之后才弄明白的,写代码的时候遇到了许多坑:
-
首先是初值问题,dp[0]到底取1还是0。刚开始没有想明白dp[n]的含义,根据上面的定义,第一次访问到0号房间是第0天,应该取0。但是程序里需要在第一次访问到房间的时候,天数加1然后赋值给dp,但是对于第0个房间,会错误地将dp[0]改为1,那么后续的天数计算就需要多加1,因为少减了1天(这个问题可以将初始的maxRoom置为0,可以回避该分支的执行)。刚开始我根据错误的初始条件,观察上面超时的用例写的状态转移方程为
dp[max] - dp[back] + 2,提交之后发现有的测试用例给出的结果比预期结果多了1,排查了半天才发现问题。 -
日期编号溢出的问题,刚开始dp与day都使用的int类型,在计算状态转移方程的时候有可能溢出,修改为long之后能够通过一些测试用例,但是后面还是会出现负值。这时我开始注意到这个问题了,就是dp保存的是取模之后的值,相减的时候会不会有问题?我们不可能无限制地扩展bit位,不可能存储准确的数值,取模是必要的。但是结果为什么还是有负值?这时灵光一闪,发现返回的负值只要加上MOD就可以得到正确的结果。这一定不是偶然的,后来才明白是因为后面的天数取模变小了,相减出现了负值,并不是溢出。但是,即便是负值一直取模,到最后返回结果的时候再加MOD也是正确的(看了官方题解,是在相减的时候加上了MOD)。
注意以下事实:
在java中进行取模运算时,结果的符号与被除数(即左边的操作数)相同:
-7 % 15 = -77 % -15 = 7-7 % -15 = -7-7 % 3 = -17 % -3 = 1-7 % -3 = -1(-7 + 15) % 15 = -7 + 15
补码(Two's Complement)是有符号数的一种二进制表示方式,主要用于计算机系统中数值的表示和存储。这种表示方式具有统一处理符号位和数值位、统一处理加法和减法的优点。
补码命名中的“2的补数”描述了补码的一个特性:一个补码可以通过被2的位长次方减去,得到它的相反数。例如,对于一个4位的补码,0001(十进制为1)的相反数可以通过计算2^4 - 0001得到,结果为1111(十进制为-1)。
在计算机中,正数的补码与其原码相同,而负数的补码则是通过对其绝对值的原码取反后加1得到。这种转换过程与原码的转换过程几乎相同,不需要额外的硬件电路。
补码的使用在电路设计上相当方便,因为只要有加法电路及补码电路,就可以完成各种有号数的加法和减法运算。
对一个正数取反加1,可以得到其相反数的补码。
对一个负数取反加1,可以得到其绝对值。因为负数a的补码就是
2^n - |a|。 其中2^n 可以想象成 n 个bit位均为1的二进制数加1。用所有bit位为1的数去减任意数就是取反,因为肯定是1变0,0变1。最后再加上多出来的1,就得到了补码。对n位2进制数(不考虑符号位)求补码其实就是求相对于2^n的补数。
-
循环的结束条件问题,最开始使用的结束条件
dp[roomNums - 1] == 0,判断是否是第一次访问使用的是dp[maxRoom] == 0。这就有问题了,第233/239个测试用例很特殊,因为结束时的天数刚好等于MOD,取模后为0,导致程序无法结束。于是后面改成了根据访问次数是否为0来判断。但是条件修改之后,访问次数在哪里累加也成了关键,如果在判断之前加就不对,牵一发而动全身。
代码
/**
* @date 2024-03-28 0:02
*/
public class FirstDayBeenInAllRooms1997 {
private static final int MOD = 1000000007;
public int firstDayBeenInAllRooms_v1(int[] nextVisit) {
int roomNums = nextVisit.length;
int[] visitCount = new int[roomNums];
long[] dp = new long[roomNums];
dp[0] = 0;
long day = 0;
int currentRoom = 0;
int maxRoom = 0;
visitCount[currentRoom] = 1;
while (visitCount[roomNums - 1] == 0) {
if (visitCount[currentRoom] % 2 == 1) {
currentRoom = nextVisit[currentRoom];
} else {
currentRoom = (currentRoom + 1) % roomNums;
maxRoom = Math.max(currentRoom, maxRoom);
}
if (visitCount[maxRoom] == 0) {
visitCount[currentRoom] += 1;
day = (day + 1) % MOD;
dp[currentRoom] = day;
} else {
if (currentRoom != maxRoom) {
day = (day + dp[maxRoom] - dp[currentRoom] + 1L) % MOD;
currentRoom = maxRoom;
} else {
day = (day + 1) % MOD;
}
visitCount[currentRoom]++;
}
}
return (int) (day < 0 ? MOD + day : day);
}
public static void main(String[] args) {
FirstDayBeenInAllRooms1997 main = new FirstDayBeenInAllRooms1997();
System.out.println(main.firstDayBeenInAllRooms_v1(new int[]{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}));
System.out.println(FastPowerMod.fastPowerMod(2, 74, MOD));
// System.out.println(main.firstDayBeenInAllRooms_v1(new int[]{0,1,2,0}));
// System.out.println(main.firstDayBeenInAllRooms_v1(new int[]{0, 0, 0, 0, 0, 0, 0, 0, 0, 9, 1, 8}));
// System.out.println(main.firstDayBeenInAllRooms_v1(new int[]{0, 0, 1, 2, 4, 0, 1, 6, 0, 0, 2, 3, 4, 3, 4, 11, 6, 0, 16, 14, 20, 16, 9, 9, 1, 8, 8, 4, 14, 13, 5, 12, 8, 18, 27, 34, 36, 13, 10, 35, 13, 31, 13, 29, 2, 45, 17, 30, 10, 18, 41, 14, 41, 22, 2, 4, 1, 15, 27, 35, 12, 10, 46, 25, 61, 8, 65, 57, 48, 61, 8, 35, 2, 66, 47, 5, 54, 76, 73, 51, 13, 64, 15, 2}));
// System.out.println(main.firstDayBeenInAllRooms_v1(new int[]{0,0,0,0,2,2,1,2,3,8,9,5,1,6,8,5,10,5,18,2,15,7,22,4,6,10,19,16,3,25,12,28,1,27,25,25,35,16,7,23,37,8,28,8,18,41,36,29}));
}性能