目标
Alice 和 Bob 正在玩一个游戏。最初,Alice 有一个字符串 word = "a"。
给定一个正整数 k 和一个整数数组 operations,其中 operations[i] 表示第 i 次操作的类型。
现在 Bob 将要求 Alice 按顺序执行 所有 操作:
- 如果 operations[i] == 0,将 word 的一份 副本追加 到它自身。
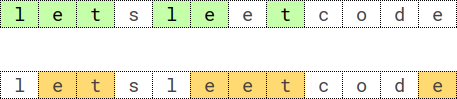
- 如果 operations[i] == 1,将 word 中的每个字符 更改 为英文字母表中的 下一个 字符来生成一个新字符串,并将其 追加 到原始的 word。例如,对 "c" 进行操作生成 "cd",对 "zb" 进行操作生成 "zbac"。
在执行所有操作后,返回 word 中第 k 个字符的值。
注意,在第二种类型的操作中,字符 'z' 可以变成 'a'。
示例 1:
输入:k = 5, operations = [0,0,0]
输出:"a"
解释:
最初,word == "a"。Alice 按以下方式执行三次操作:
将 "a" 附加到 "a",word 变为 "aa"。
将 "aa" 附加到 "aa",word 变为 "aaaa"。
将 "aaaa" 附加到 "aaaa",word 变为 "aaaaaaaa"。示例 2:
输入:k = 10, operations = [0,1,0,1]
输出:"b"
解释:
最初,word == "a"。Alice 按以下方式执行四次操作:
将 "a" 附加到 "a",word 变为 "aa"。
将 "bb" 附加到 "aa",word 变为 "aabb"。
将 "aabb" 附加到 "aabb",word 变为 "aabbaabb"。
将 "bbccbbcc" 附加到 "aabbaabb",word 变为 "aabbaabbbbccbbcc"。说明:
- 1 <= k <= 10^14
- 1 <= operations.length <= 100
- operations[i] 可以是 0 或 1。
- 输入保证在执行所有操作后,word 至少有 k 个字符。
思路
开始的时候有一个字符 a,根据操作数组 operations 执行以下操作:
- 当
operations[i] == 0时,将现有的所有字母拼接到当前字符后面。 - 当
operations[i] == 1时,将现有的所有字母替换为它在字母表中的下一个字母(z的下一个字母为a),拼接到当前字符后面。
返回执行所有操作之后的第 k 个字母。
计算 tail = ceil(log2(k)) 表示操作次数的上界,如果 k <= 1 << tail,说明在左半边无需操作,否则在右半边,需要操作,它是从左半边的第 k - (1 << tail) 个元素转移而来,需要根据 operations[tail] 来确定字母是否变化。按照这个逻辑递归,直到 tail < 0,返回字母 a。
代码
/**
* @date 2025-07-04 9:19
*/
public class KthCharacter3307 {
public char kthCharacter(long k, int[] operations) {
return kthCharacter(k, operations, 63 - Long.numberOfLeadingZeros(k - 1));
}
public char kthCharacter(long k, int[] operations, int tail) {
if (tail < 0) {
return 'a';
}
long p = 1L << tail;
if (k <= p) {
return (char) ('a' + ((kthCharacter(k, operations, tail - 1) - 'a') % 26));
}
return (char) ('a' + (kthCharacter(k - p, operations, tail - 1) - 'a' + operations[tail]) % 26);
}
}
性能