目标
由于一个漏洞,文件系统中存在许多重复文件夹。给你一个二维数组 paths,其中 paths[i] 是一个表示文件系统中第 i 个文件夹的绝对路径的数组。
例如,["one", "two", "three"] 表示路径 "/one/two/three" 。
如果两个文件夹(不需要在同一层级)包含 非空且相同的 子文件夹 集合 并具有相同的子文件夹结构,则认为这两个文件夹是相同文件夹。相同文件夹的根层级 不 需要相同。如果存在两个(或两个以上)相同 文件夹,则需要将这些文件夹和所有它们的子文件夹 标记 为待删除。
例如,下面文件结构中的文件夹 "/a" 和 "/b" 相同。它们(以及它们的子文件夹)应该被 全部 标记为待删除:
- /a
- /a/x
- /a/x/y
- /a/z
- /b
- /b/x
- /b/x/y
- /b/z
然而,如果文件结构中还包含路径 "/b/w" ,那么文件夹 "/a" 和 "/b" 就不相同。注意,即便添加了新的文件夹 "/b/w" ,仍然认为 "/a/x" 和 "/b/x" 相同。
一旦所有的相同文件夹和它们的子文件夹都被标记为待删除,文件系统将会 删除 所有上述文件夹。文件系统只会执行一次删除操作。执行完这一次删除操作后,不会删除新出现的相同文件夹。
返回二维数组 ans ,该数组包含删除所有标记文件夹之后剩余文件夹的路径。路径可以按 任意顺序 返回。
示例 1:
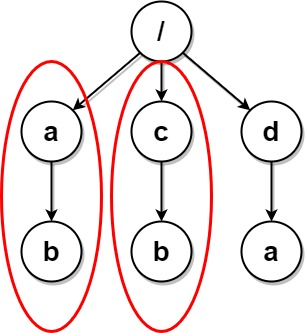
输入:paths = [["a"],["c"],["d"],["a","b"],["c","b"],["d","a"]]
输出:[["d"],["d","a"]]
解释:文件结构如上所示。
文件夹 "/a" 和 "/c"(以及它们的子文件夹)都会被标记为待删除,因为它们都包含名为 "b" 的空文件夹。
示例 2:
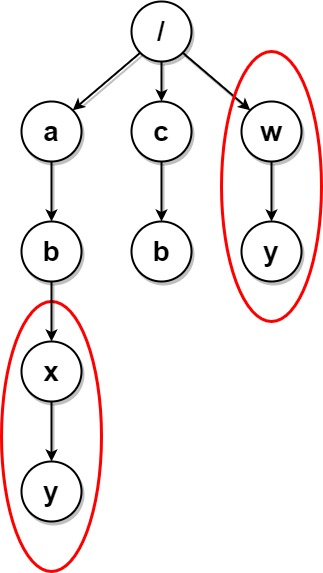
输入:paths = [["a"],["c"],["a","b"],["c","b"],["a","b","x"],["a","b","x","y"],["w"],["w","y"]]
输出:[["c"],["c","b"],["a"],["a","b"]]
解释:文件结构如上所示。
文件夹 "/a/b/x" 和 "/w"(以及它们的子文件夹)都会被标记为待删除,因为它们都包含名为 "y" 的空文件夹。
注意,文件夹 "/a" 和 "/c" 在删除后变为相同文件夹,但这两个文件夹不会被删除,因为删除只会进行一次,且它们没有在删除前被标记。
示例 3:
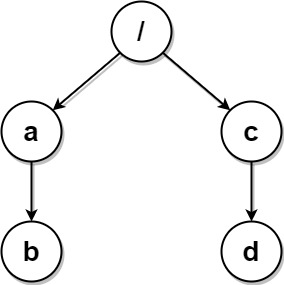
输入:paths = [["a","b"],["c","d"],["c"],["a"]]
输出:[["c"],["c","d"],["a"],["a","b"]]
解释:文件系统中所有文件夹互不相同。
注意,返回的数组可以按不同顺序返回文件夹路径,因为题目对顺序没有要求。
示例 4:
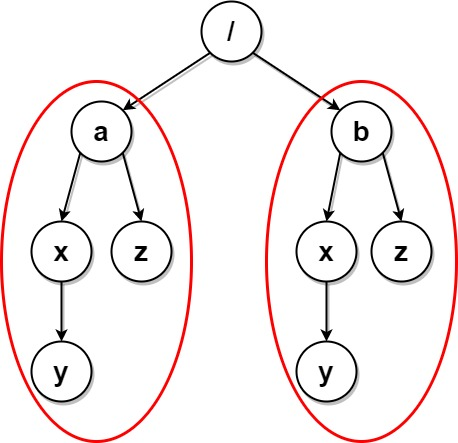
输入:paths = [["a"],["a","x"],["a","x","y"],["a","z"],["b"],["b","x"],["b","x","y"],["b","z"]]
输出:[]
解释:文件结构如上所示。
文件夹 "/a/x" 和 "/b/x"(以及它们的子文件夹)都会被标记为待删除,因为它们都包含名为 "y" 的空文件夹。
文件夹 "/a" 和 "/b"(以及它们的子文件夹)都会被标记为待删除,因为它们都包含一个名为 "z" 的空文件夹以及上面提到的文件夹 "x" 。
示例 5:
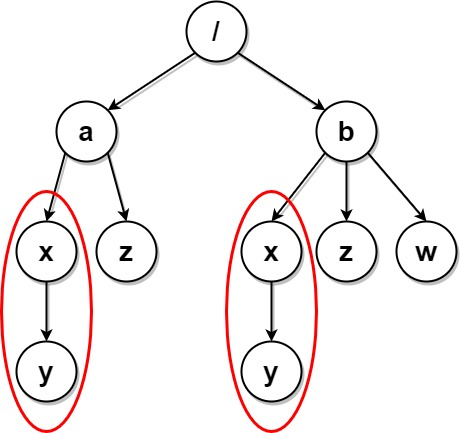
输入:paths = [["a"],["a","x"],["a","x","y"],["a","z"],["b"],["b","x"],["b","x","y"],["b","z"],["b","w"]]
输出:[["b"],["b","w"],["b","z"],["a"],["a","z"]]
解释:本例与上例的结构基本相同,除了新增 "/b/w" 文件夹。
文件夹 "/a/x" 和 "/b/x" 仍然会被标记,但 "/a" 和 "/b" 不再被标记,因为 "/b" 中有名为 "w" 的空文件夹而 "/a" 没有。
注意,"/a/z" 和 "/b/z" 不会被标记,因为相同子文件夹的集合必须是非空集合,但这两个文件夹都是空的。
说明:
- 1 <= paths.length <= 2 * 10^4
- 1 <= paths[i].length <= 500
- 1 <= paths[i][j].length <= 10
- 1 <= sum(paths[i][j].length) <= 2 * 10^5
- path[i][j] 由小写英文字母组成
- 不会存在两个路径都指向同一个文件夹的情况
- 对于不在根层级的任意文件夹,其父文件夹也会包含在输入中
思路
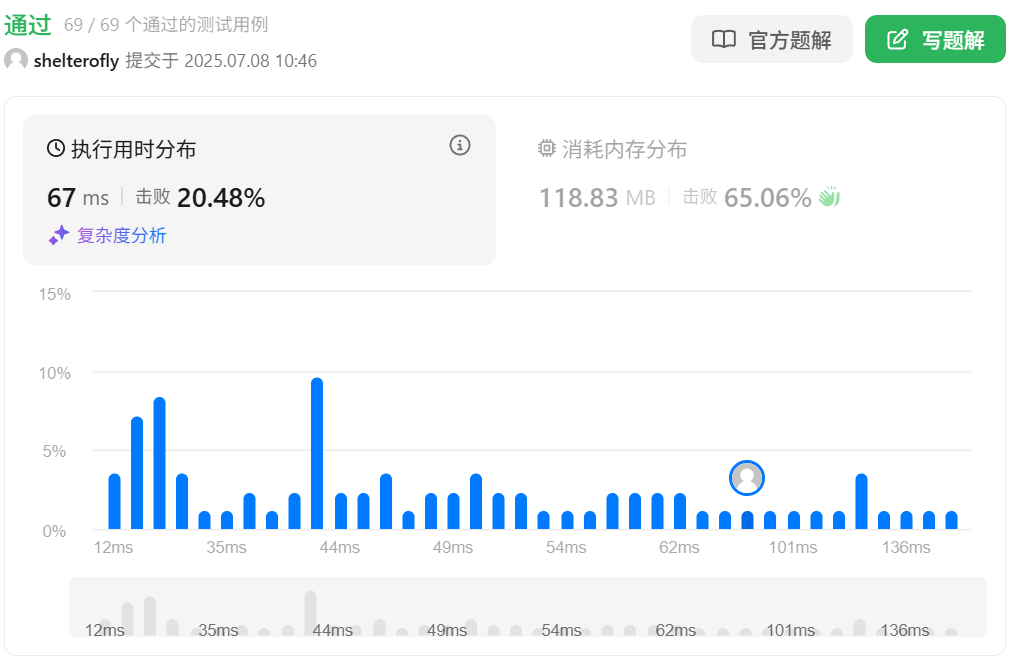
代码
性能