目标
给你一个整数数组 nums 和两个整数 k 和 numOperations 。
你必须对 nums 执行 操作 numOperations 次。每次操作中,你可以:
- 选择一个下标 i ,它在之前的操作中 没有 被选择过。
- 将 nums[i] 增加范围 [-k, k] 中的一个整数。
在执行完所有操作以后,请你返回 nums 中出现 频率最高 元素的出现次数。
一个元素 x 的 频率 指的是它在数组中出现的次数。
示例 1:
输入:nums = [1,4,5], k = 1, numOperations = 2
输出:2
解释:
通过以下操作得到最高频率 2 :
将 nums[1] 增加 0 ,nums 变为 [1, 4, 5] 。
将 nums[2] 增加 -1 ,nums 变为 [1, 4, 4] 。示例 2:
输入:nums = [5,11,20,20], k = 5, numOperations = 1
输出:2
解释:
通过以下操作得到最高频率 2 :
将 nums[1] 增加 0 。说明:
- 1 <= nums.length <= 10^5
- 1 <= nums[i] <= 10^9
- 0 <= k <= 10^9
- 0 <= numOperations <= nums.length
思路
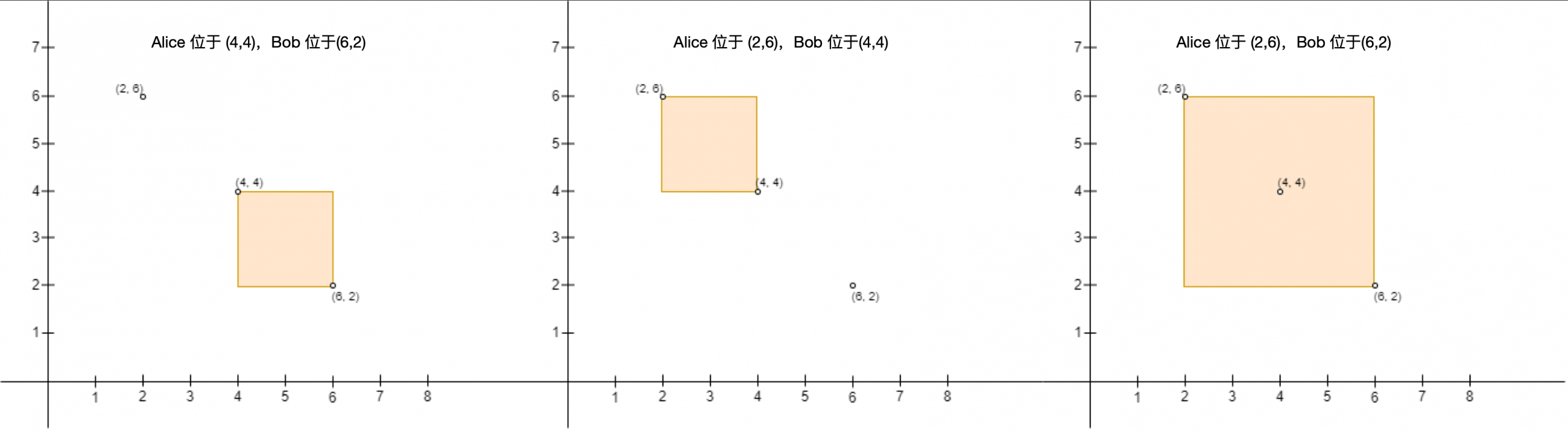
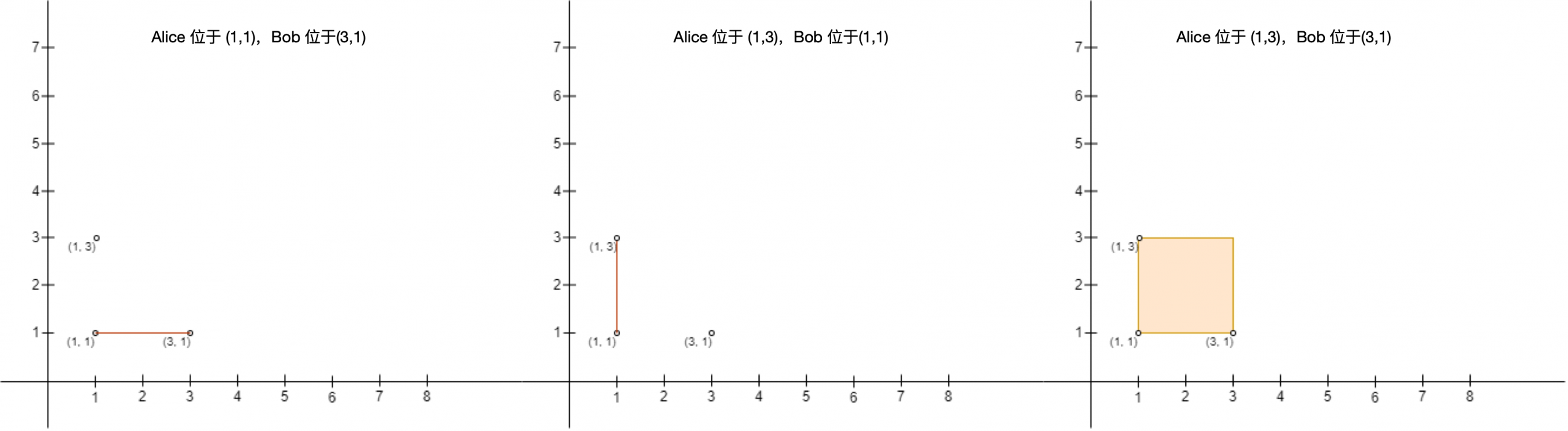
对数组 nums 执行 numOperations 次操作,每次操作可以选一个没有被操作过的元素,将其增加 [-k, k] 之间的整数,求元素值的最大出现次数。
与 3346.执行操作后元素的最高频率I 相比,本题的数据范围更大,无法枚举值域。
考虑使用差分数组,由于数据范围太大,使用有序集合来维护。差分数组的前缀就是可以操作成该元素的频率,它不能超过原来已有的个数 + 操作次数。
代码
/**
* @date 2025-10-21 10:34
*/
public class MaxFrequency3347 {
public int maxFrequency(int[] nums, int k, int numOperations) {
Map<Integer, Integer> cnt = new HashMap<>();
Map<Integer, Integer> diff = new TreeMap<>();
for (int num : nums) {
cnt.merge(num, 1, Integer::sum);
diff.putIfAbsent(num, 0);
diff.merge(num - k, 1, Integer::sum);
diff.merge(num + k + 1, -1, Integer::sum);
}
int res = 0;
int frequency = 0;
for (Map.Entry<Integer, Integer> entry : diff.entrySet()) {
frequency += entry.getValue();
res = Math.max(res, Math.min(frequency, cnt.getOrDefault(entry.getKey(), 0) + numOperations));
}
return res;
}
}
性能