目标
有 n 个 (id, value) 对,其中 id 是 1 到 n 之间的一个整数,value 是一个字符串。不存在 id 相同的两个 (id, value) 对。
设计一个流,以 任意 顺序获取 n 个 (id, value) 对,并在多次调用时 按 id 递增的顺序 返回一些值。
实现 OrderedStream 类:
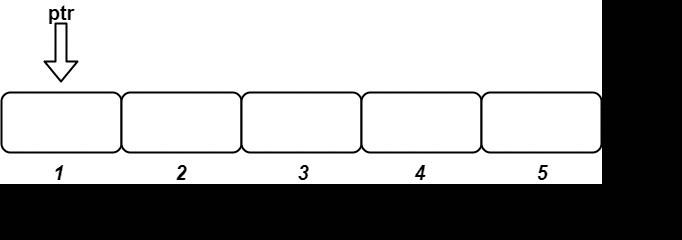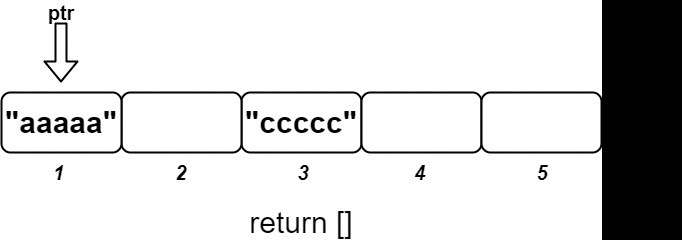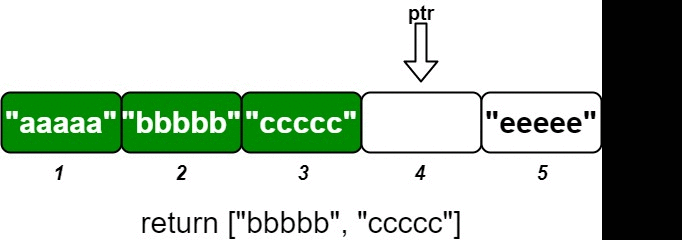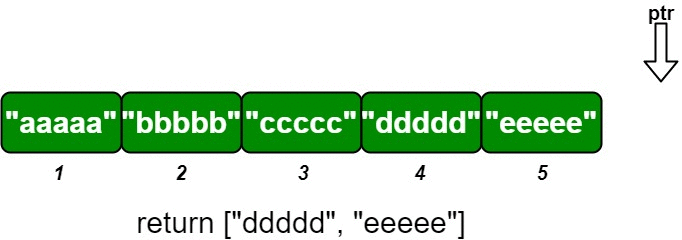
- OrderedStream(int n) 构造一个能接收 n 个值的流,并将当前指针 ptr 设为 1 。
- String[] insert(int id, String value) 向流中存储新的 (id, value) 对。存储后:
- 如果流存储有 id = ptr 的 (id, value) 对,则找出从 id = ptr 开始的 最长 id 连续递增序列 ,并 按顺序 返回与这些 id 关联的值的列表。然后,将 ptr 更新为最后那个 id + 1 。
- 否则,返回一个空列表。
示例:
输入
["OrderedStream", "insert", "insert", "insert", "insert", "insert"]
[[5], [3, "ccccc"], [1, "aaaaa"], [2, "bbbbb"], [5, "eeeee"], [4, "ddddd"]]
输出
[null, [], ["aaaaa"], ["bbbbb", "ccccc"], [], ["ddddd", "eeeee"]]
解释
OrderedStream os= new OrderedStream(5);
os.insert(3, "ccccc"); // 插入 (3, "ccccc"),返回 []
os.insert(1, "aaaaa"); // 插入 (1, "aaaaa"),返回 ["aaaaa"]
os.insert(2, "bbbbb"); // 插入 (2, "bbbbb"),返回 ["bbbbb", "ccccc"]
os.insert(5, "eeeee"); // 插入 (5, "eeeee"),返回 []
os.insert(4, "ddddd"); // 插入 (4, "ddddd"),返回 ["ddddd", "eeeee"]说明:
- 1 <= n <= 1000
- 1 <= id <= n
- value.length == 5
- value 仅由小写字母组成
- 每次调用 insert 都会使用一个唯一的 id
- 恰好调用 n 次 insert
思路
将编号为 id 的数据放入对应的位置上,pos 从 0 开始,如果 pos 位置上有数据,就输出自身及其后面非空的数据。
代码
/**
* @date 2025-02-24 8:50
*/
public class OrderedStream1656 {
static class OrderedStream {
private final String[] buffer;
private int pos = 1;
public OrderedStream(int n) {
buffer = new String[n + 1];
}
public List<String> insert(int idKey, String value) {
List<String> res = new ArrayList<>();
if (idKey != pos) {
buffer[idKey] = value;
return res;
}
buffer[pos] = value;
while (pos < buffer.length && buffer[pos] != null) {
res.add(buffer[pos++]);
}
return res;
}
}
}
性能