目标
「力扣挑战赛」心算项目的挑战比赛中,要求选手从 N 张卡牌中选出 cnt 张卡牌,若这 cnt 张卡牌数字总和为偶数,则选手成绩「有效」且得分为 cnt 张卡牌数字总和。 给定数组 cards 和 cnt,其中 cards[i] 表示第 i 张卡牌上的数字。 请帮参赛选手计算最大的有效得分。若不存在获取有效得分的卡牌方案,则返回 0。
示例 1:
输入:cards = [1,2,8,9], cnt = 3
输出:18
解释:选择数字为 1、8、9 的这三张卡牌,此时可获得最大的有效得分 1+8+9=18。示例 2:
输入:cards = [3,3,1], cnt = 1
输出:0
解释:不存在获取有效得分的卡牌方案。说明:
- 1 <= cnt <= cards.length <= 10^5
- 1 <= cards[i] <= 1000
思路
从数组中选cnt个元素,找出最大的偶数和,如果不存在偶数和返回0。
如果cnt为偶数,那么直接取最大的cnt个即可,如果cnt为奇数,取最大的cnt-1个,然后再从大到小判断和是否为偶数即可。 与cnt的奇偶性无关,它也不能保证cnt个元素相加和为偶数,必须要奇数元素的个数为偶数才行。
应该使用动态规划来做了,O(cnt * n)超出时间限制。
尝试根据数组元素奇偶性分组,然后分情况讨论如何选取。这里的限制条件是必须选取偶数个奇数元素,并且使得和最大。
这道题标成简单真的搞人心态啊,还是做的太少了。
代码
/**
* @date 2024-08-01 20:24
*/
public class MaxmiumScoreLCP40 {
public int maxmiumScore_v2(int[] cards, int cnt) {
int res = 0;
PriorityQueue<Integer> odd = new PriorityQueue<>((a, b) -> b - a);
PriorityQueue<Integer> even = new PriorityQueue<>((a, b) -> b - a);
// 将奇偶元素分组
for (int card : cards) {
if (card % 2 == 0) {
even.offer(card);
} else {
odd.offer(card);
}
}
// 如果只能选一个元素,那么直接从偶数队列取,否则返回0
if (cnt == 1 && even.size() > 0) {
return even.poll();
} else if (cnt == 1) {
return 0;
}
int oddCnt = 0;
int lastOdd = 0;
int lastEven = 0;
// 从奇偶队列中,从大到小取cnt-1个,留一个后面分情况讨论
while (cnt > 1) {
if (!odd.isEmpty() && !even.isEmpty() && odd.peek() > even.peek()) {
lastOdd = odd.poll();
res += lastOdd;
oddCnt++;
} else if (!odd.isEmpty() && !even.isEmpty()) {
lastEven = even.poll();
res += lastEven;
} else if (!odd.isEmpty()) {
lastOdd = odd.poll();
res += lastOdd;
oddCnt++;
} else if (!even.isEmpty()) {
lastEven = even.poll();
res += lastEven;
}
cnt--;
}
if (oddCnt % 2 == 1 && !odd.isEmpty()) {
// 如果选择了奇数个奇数元素,并且奇数队列还有剩余元素
if (even.size() >= 2) {
// 如果偶数队列有超过两个,并且这两个之和大于最近已选的奇数元素+奇数队列的元素
int tmp = even.poll();
tmp += even.poll();
if (tmp > lastOdd + odd.peek()) {
// 将上一个奇数选择删除,选两个偶数
res += tmp - lastOdd;
} else {
// 否则选一个奇数
res += odd.poll();
}
} else {
// 如果没有多余的偶数元素,直接选一个奇数
res += odd.poll();
}
} else if (oddCnt % 2 == 1 && even.size() >= 2) {
// 如果已经选了奇数个奇数元素,并且没有多余的奇数元素了,那么回退,选两个偶数
res -= lastOdd;
res += even.poll();
res += even.poll();
} else if (oddCnt % 2 == 0) {
// 如果奇数元素选了偶数个,那么只需再选一个偶数,或者删掉一个偶数,选两个奇数
if (odd.size() >= 2 && lastEven != 0) {
// 如果奇数存在两个,且之前选过偶数
int tmp = odd.poll();
tmp += odd.poll();
if (even.size() == 0 || tmp > lastEven + even.peek()) {
// 如果没有多余的偶数,或者两个奇数之和大于之前选择的偶数+偶数队列元素
// 选两个奇数
res += tmp - lastEven;
} else {
// 选一个偶数
res += even.poll();
}
} else {
// 如果没有多余2个的奇数了,只能选一个偶数
if (even.size() == 0) {
return 0;
} else {
res += even.poll();
}
}
} else {
// 如果已经选了奇数个奇数元素,并且没有多余的奇数元素了,并且偶数个数不足2个,返回0
res = 0;
}
return res;
}
}
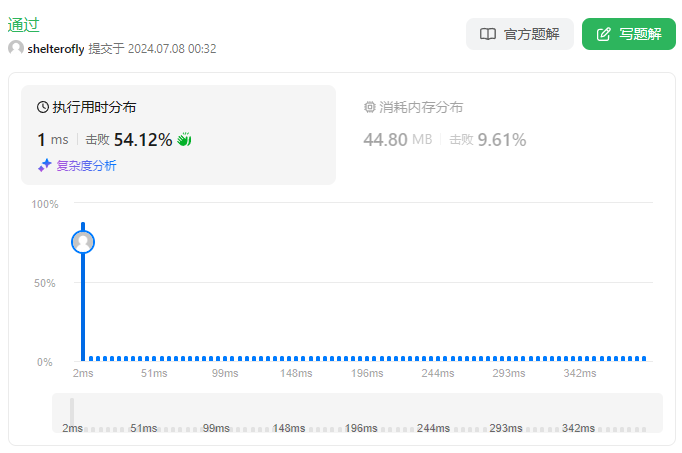
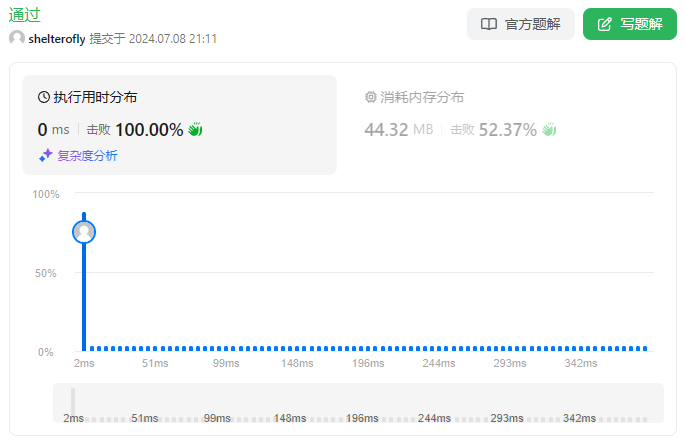
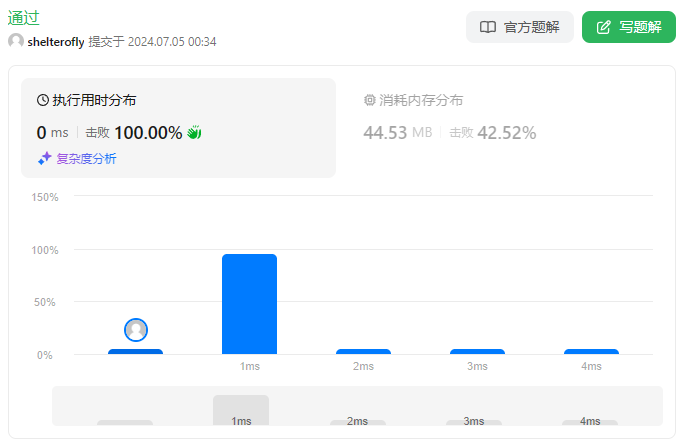
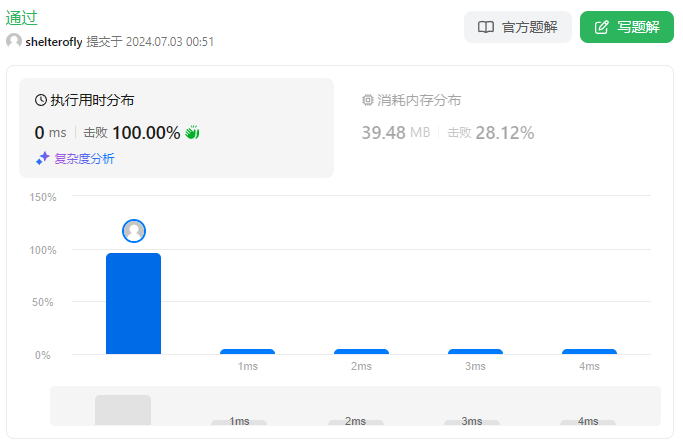
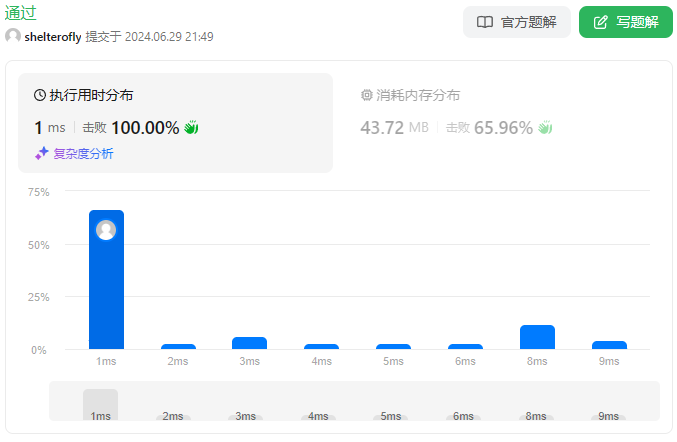
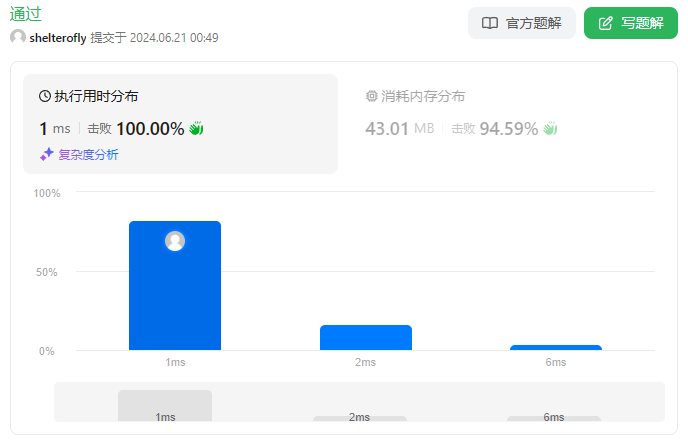
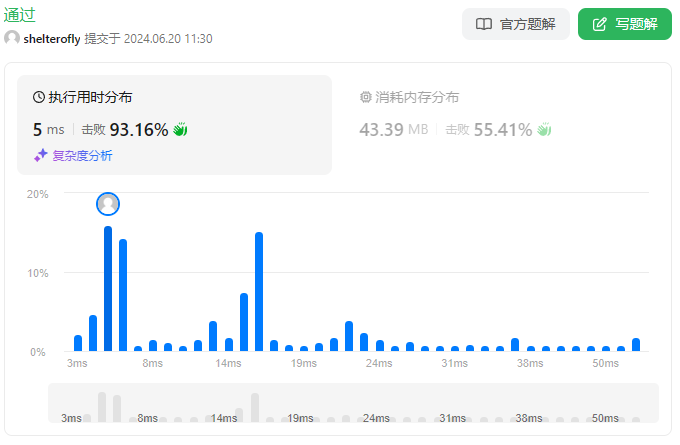
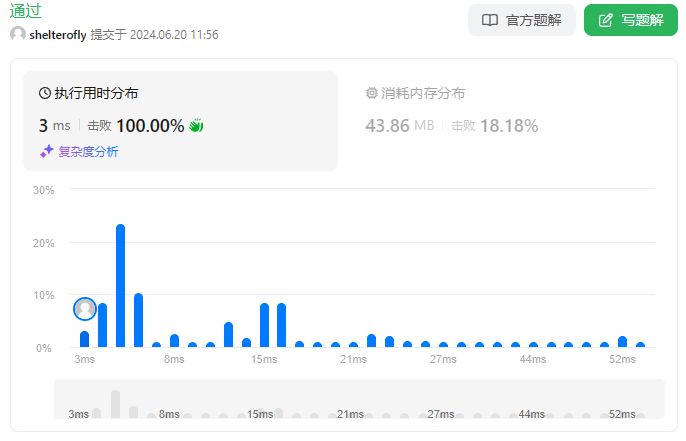
性能