目标
给你一个整数 n ,表示在一个游戏中的玩家数目。同时给你一个二维整数数组 pick ,其中 pick[i] = [xi, yi] 表示玩家 xi 获得了一个颜色为 yi 的球。
如果玩家 i 获得的球中任何一种颜色球的数目 严格大于 i 个,那么我们说玩家 i 是胜利玩家。换句话说:
- 如果玩家 0 获得了任何的球,那么玩家 0 是胜利玩家。
- 如果玩家 1 获得了至少 2 个相同颜色的球,那么玩家 1 是胜利玩家。
- ...
- 如果玩家 i 获得了至少 i + 1 个相同颜色的球,那么玩家 i 是胜利玩家。
请你返回游戏中 胜利玩家 的数目。
注意,可能有多个玩家是胜利玩家。
示例 1:
输入:n = 4, pick = [[0,0],[1,0],[1,0],[2,1],[2,1],[2,0]]
输出:2
解释:
玩家 0 和玩家 1 是胜利玩家,玩家 2 和玩家 3 不是胜利玩家。示例 2:
输入:n = 5, pick = [[1,1],[1,2],[1,3],[1,4]]
输出:0
解释:
没有胜利玩家。示例 3:
输入:n = 5, pick = [[1,1],[2,4],[2,4],[2,4]]
输出:1
解释:
玩家 2 是胜利玩家,因为玩家 2 获得了 3 个颜色为 4 的球。说明:
- 2 <= n <= 10
- 1 <= pick.length <= 100
- pick[i].length == 2
- 0 <= xi <= n - 1
- 0 <= yi <= 10
思路
有 n 个玩家,pick[i][j] 表示第 i 次操作,玩家 pick[i][0] 捡起了颜色为 pick[i][1] 的球,如果玩家 pick[i][0] 捡起同一颜色球的数量大于 pick[i][0] 则胜出,求胜出玩家的总数。
只要达到条件就胜出,并不是零和游戏。玩家与球的颜色是一对多的关系,并且需要针对每种颜色计数,判断是否存在某些颜色球的个数 大于 玩家编号。
使用二维数组 playerBall[i][c] 表示玩家 i 捡起颜色为 c 的球的数目,遍历 pick 数组计算 playerBall[i][c],然后遍历 playerBall 统计胜出玩家的数目。
代码
/**
* @date 2024-11-23 14:17
*/
public class WinningPlayerCount3238 {
public int winningPlayerCount(int n, int[][] pick) {
int[][] playerBall = new int[n][11];
for (int i = 0; i < pick.length; i++) {
// pick的i表示的是操作次数,j为0表示用户,j为1表示球的颜色
playerBall[pick[i][0]][pick[i][1]]++;
}
int res = 0;
for (int i = 0; i < playerBall.length; i++) {
for (int j = 0; j < playerBall[i].length; j++) {
if (playerBall[i][j] > i){
res++;
break;
}
}
}
return res;
}
}
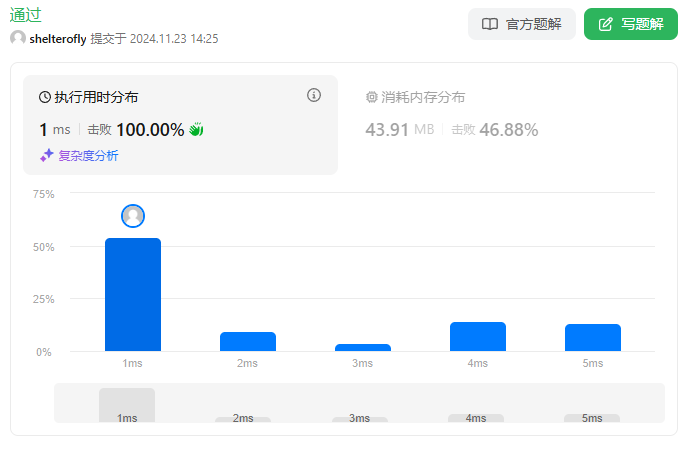
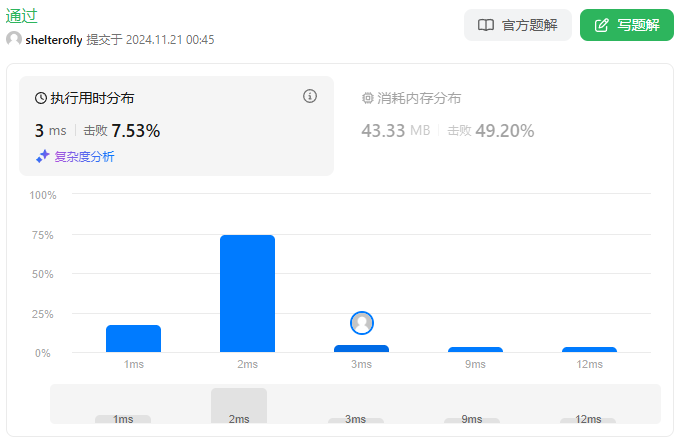
性能