标签： dfs

目标

给定一个根为 root 的二叉树，每个节点的深度是 该节点到根的最短距离 。

返回包含原始树中所有 最深节点 的 最小子树 。

如果一个节点在 整个树 的任意节点之间具有最大的深度，则该节点是 最深的 。

一个节点的 子树 是该节点加上它的所有后代的集合。

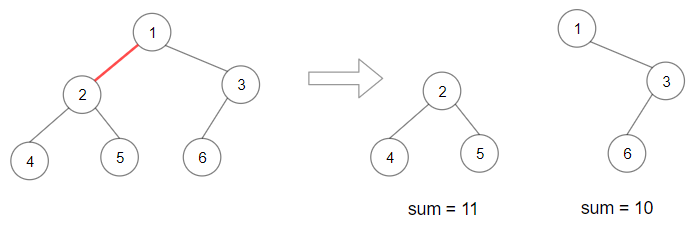
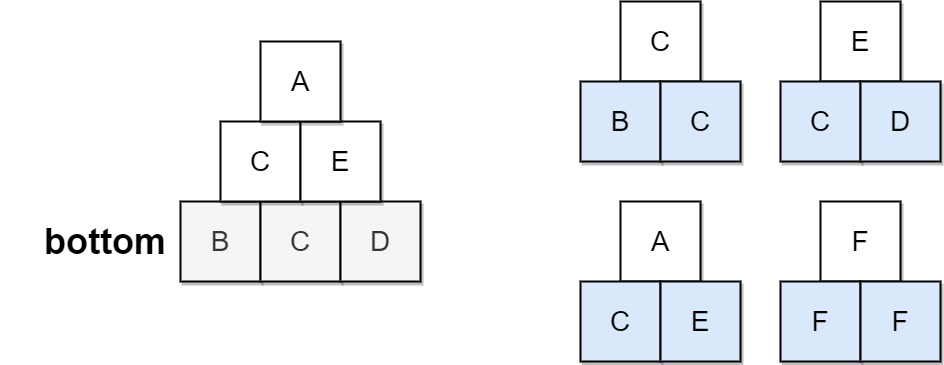
示例 1：

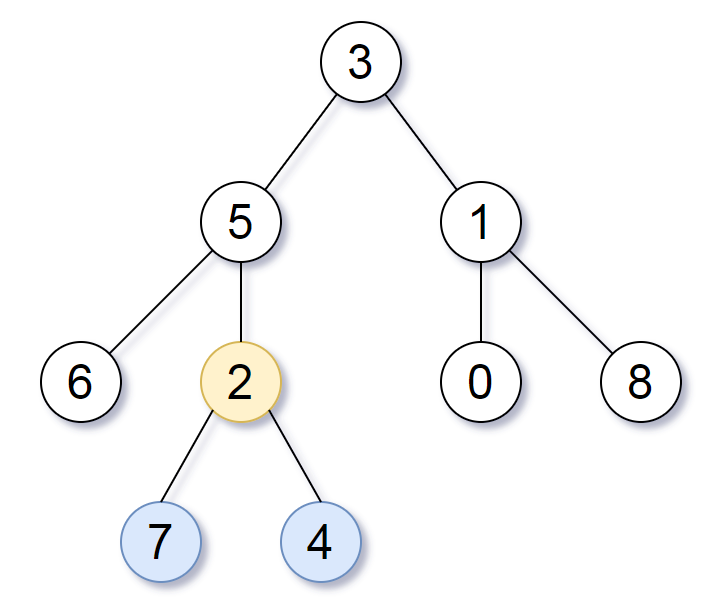
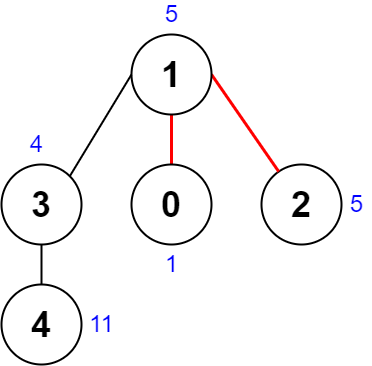
输入：root = [3,5,1,6,2,0,8,null,null,7,4]
输出：[2,7,4]
解释：
我们返回值为 2 的节点，在图中用黄色标记。
在图中用蓝色标记的是树的最深的节点。
注意，节点 5、3 和 2 包含树中最深的节点，但节点 2 的子树最小，因此我们返回它。

示例 2：

输入：root = [1]
输出：[1]
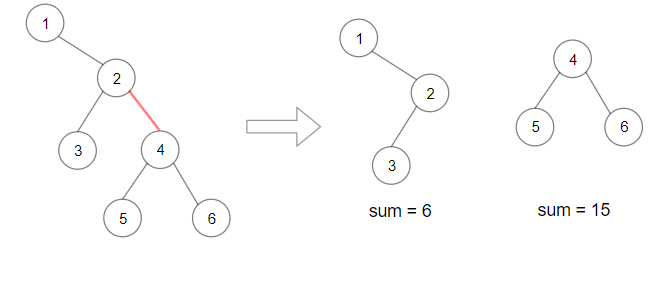
解释：根节点是树中最深的节点。

示例 3：

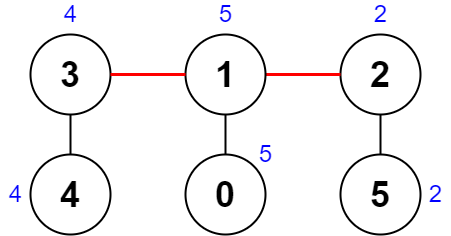
输入：root = [0,1,3,null,2]
输出：[2]
解释：树中最深的节点为 2 ，有效子树为节点 2、1 和 0 的子树，但节点 2 的子树最小。

说明：

• 树中节点的数量在 [1, 500] 范围内。
• 0 <= Node.val <= 500
• 每个节点的值都是 独一无二 的。

思路

有一颗二叉树 root，返回包含所有最深节点的最小子树。

dfs 返回子树最大深度，如果左右子树的深度都等于全局的最大深度，则返回当前节点。也就是找到所有最深节点的最近公共祖先。

代码

/**
 * @date 2026-01-09 8:45
 */
public class SubtreeWithAllDeepest865 {

    public TreeNode subtreeWithAllDeepest(TreeNode root) {
        dfs(root, -1);
        return res;
    }

    public int dfs(TreeNode node, int deep) {
        if (node == null) {
            return deep;
        }
        int left = dfs(node.left, deep + 1);
        int right = dfs(node.right, deep + 1);
        int max = Math.max(left, right);
        maxDeep = Math.max(max, maxDeep);
        if (left == maxDeep && right == maxDeep) {
            res = node;
        }
        return max;
    }

}

性能

目标

给你一棵二叉树，它的根为 root 。请你删除 1 条边，使二叉树分裂成两棵子树，且它们子树和的乘积尽可能大。

由于答案可能会很大，请你将结果对 10^9 + 7 取模后再返回。

示例 1：

输入：root = [1,2,3,4,5,6]
输出：110
解释：删除红色的边，得到 2 棵子树，和分别为 11 和 10 。它们的乘积是 110 （11*10）

示例 2：

输入：root = [1,null,2,3,4,null,null,5,6]
输出：90
解释：移除红色的边，得到 2 棵子树，和分别是 15 和 6 。它们的乘积为 90 （15*6）

示例 3：

输入：root = [2,3,9,10,7,8,6,5,4,11,1]
输出：1025

示例 4：

输入：root = [1,1]
输出：1

说明：

• 每棵树最多有 50000 个节点，且至少有 2 个节点。
• 每个节点的值在 [1, 10000] 之间。

思路

删除二叉树的一条边，使得产生的两个子树和的乘积最大。

直接的想法是两次遍历，第一次遍历求得所有节点和。第二次遍历则是计算乘积最大值。

可以将子树和保存起来，遍历结束后直接处理和。

注意：求的是最大的乘积然后取模，而非模的最大值。先找出最大的乘积再取模，不能先对乘积取模再比较。

代码

/**
 * @date 2026-01-07 8:52
 */
public class MaxProduct1339 {

    public long res = 0L;

    public int maxProduct(TreeNode root) {
        int mod = 1000000007;
        int totalSum = dfs(root);
        dfs(root, totalSum);
        return (int) (res % mod);
    }

    public int dfs(TreeNode node) {
        if (node == null) {
            return 0;
        }
        return node.val + dfs(node.left) + dfs(node.right);
    }

    public int dfs(TreeNode node, int totalSum) {
        if (node == null) {
            return 0;
        }
        int sum = node.val + dfs(node.left, totalSum) + dfs(node.right, totalSum);
        res = Math.max(res, (long) sum * (totalSum - sum));
        return sum;
    }

}

性能

目标

你正在把积木堆成金字塔。每个块都有一个颜色，用一个字母表示。每一行的块比它下面的行 少一个块 ，并且居中。

为了使金字塔美观，只有特定的 三角形图案 是允许的。一个三角形的图案由 两个块 和叠在上面的 单个块 组成。模式是以三个字母字符串的列表形式 allowed 给出的，其中模式的前两个字符分别表示左右底部块，第三个字符表示顶部块。

• 例如，"ABC" 表示一个三角形图案，其中一个 “C” 块堆叠在一个 'A' 块(左)和一个 'B' 块(右)之上。请注意，这与 "BAC" 不同，"B" 在左下角，"A" 在右下角。

你从作为单个字符串给出的底部的一排积木 bottom 开始，必须 将其作为金字塔的底部。

在给定 bottom 和 allowed 的情况下，如果你能一直构建到金字塔顶部，使金字塔中的 每个三角形图案 都是在 allowed 中的，则返回 true ，否则返回 false 。

示例 1：

输入：bottom = "BCD", allowed = ["BCC","CDE","CEA","FFF"]
输出：true
解释：允许的三角形图案显示在右边。
从最底层(第 3 层)开始，我们可以在第 2 层构建“CE”，然后在第 1 层构建“E”。
金字塔中有三种三角形图案，分别是 “BCC”、“CDE” 和 “CEA”。都是允许的。

示例 2：

输入：bottom = "AAAA", allowed = ["AAB","AAC","BCD","BBE","DEF"]
输出：false
解释：允许的三角形图案显示在右边。
从最底层(即第 4 层)开始，创造第 3 层有多种方法，但如果尝试所有可能性，你便会在创造第 1 层前陷入困境。

说明：

• 2 <= bottom.length <= 6
• 0 <= allowed.length <= 216
• allowed[i].length == 3
• 所有输入字符串中的字母来自集合 {'A', 'B', 'C', 'D', 'E', 'F'}。
• allowed 中所有值都是 唯一的

思路

有一排积木 bottom，将其作为金字塔的底部，又有一个模式列表 allowed，每个模式是一个长度为 3 的字符串 pattern，表示 pattern[2] 堆叠在左侧的 pattern[0] 和右侧的 pattern[1] 之上。判断能否使用给定的模式堆成一个金字塔。

使用哈希表保存 pattern 下面两个与上面一个的对应关系，dfs 暴力枚举所有可能，分为两个维度，枚举当前层所有可能的排列，生成下一层所有可能的排列；枚举特定的上一层排列生成对应可能的排列。

代码

/**
 * @date 2025-12-29 9:23
 */
public class PyramidTransition756 {

    public boolean pyramidTransition(String bottom, List<String> allowed) {
        int n = bottom.length();
        Map<String, Set<Character>> map = new HashMap<>();
        for (String s : allowed) {
            String key = s.substring(0, 2);
            map.putIfAbsent(key, new HashSet<>());
            map.get(key).add(s.charAt(2));
        }
        Set<String> candidates = new HashSet<>();
        candidates.add(bottom);
        Set<String> top = dfs(1, n, map, candidates);
        return top.size() > 0;
    }

    public Set<String> dfs(int l, int n, Map<String, Set<Character>> map, Set<String> candidates) {
        if (l == n) {
            return candidates;
        }
        Set<String> next = new HashSet<>();
        for (String prev : candidates) {
            Set<String> tmp = new HashSet<>();
            dfs(1, prev, "", map, tmp);
            next.addAll(tmp);
        }
        return dfs(l + 1, n, map, next);
    }

    public void dfs(int index, String prev, String row, Map<String, Set<Character>> map, Set<String> set) {
        if (index == prev.length()) {
            if (!"".equals(row)) {
                set.add(row);
            }
            return;
        }
        String key = prev.charAt(index - 1) + String.valueOf(prev.charAt(index));
        Set<Character> characters = map.get(key);
        if (characters != null) {
            for (Character c : characters) {
                dfs(index + 1, prev, row + c, map, set);
            }
        }
    }

}

性能

目标

给你一个整数 n ，如果你可以将 n 表示成若干个 不同的 三的幂之和，请你返回 true ，否则请返回 false 。

对于一个整数 y ，如果存在整数 x 满足 y == 3x ，我们称这个整数 y 是三的幂。

示例 1：

输入：n = 12
输出：true
解释：12 = 31 + 32

示例 2：

输入：n = 91
输出：true
解释：91 = 30 + 32 + 34

示例 3：

输入：n = 21
输出：false

提示：

• 1 <= n <= 10^7

思路

判断一个整数 n 能否用若干个 不同的 3 的幂之和表示。

直接的想法是使用 dfs 从小到大判断 3 的幂选或者不选。

从数学的角度考虑，如果 n 的三进制表示中包含 2 那么就无法用不同的三的幂之和表示。

代码

/**
 * @date 2025-08-14 9:54
 */
public class CheckPowersOfThree1780 {

    class Solution {
        public boolean checkPowersOfThree(int n) {
            while (n > 0) {
                if (n % 3 == 2) {
                    return false;
                }
                n /= 3;
            }
            return true;
        }
    }

    public boolean checkPowersOfThree(int n) {
        return dfs(1, 0, n);
    }

    public boolean dfs(int d, int num, int n) {
        if (num == n) {
            return true;
        } else if (num > n || d > n) {
            return false;
        }
        return dfs(d * 3, num, n) || dfs(d * 3, num + d, n);
    }

}

性能

目标

给你一个整数数组 nums ，请你找出 nums 子集 按位或 可能得到的 最大值 ，并返回按位或能得到最大值的 不同非空子集的数目 。

如果数组 a 可以由数组 b 删除一些元素（或不删除）得到，则认为数组 a 是数组 b 的一个 子集 。如果选中的元素下标位置不一样，则认为两个子集 不同 。

对数组 a 执行 按位或 ，结果等于 a[0] OR a[1] OR ... OR a[a.length - 1]（下标从 0 开始）。

示例 1：

输入：nums = [3,1]
输出：2
解释：子集按位或能得到的最大值是 3 。有 2 个子集按位或可以得到 3 ：
- [3]
- [3,1]

示例 2：

输入：nums = [2,2,2]
输出：7
解释：[2,2,2] 的所有非空子集的按位或都可以得到 2 。总共有 23 - 1 = 7 个子集。

示例 3：

输入：nums = [3,2,1,5]
输出：6
解释：子集按位或可能的最大值是 7 。有 6 个子集按位或可以得到 7 ：
- [3,5]
- [3,1,5]
- [3,2,5]
- [3,2,1,5]
- [2,5]
- [2,1,5]

说明：

• 1 <= nums.length <= 16
• 1 <= nums[i] <= 10^5

思路

统计数组按位或得到最大值的子集数目。

显然最大值是所有元素按位或，dfs 枚举元素选或不选，看或值是否最大。

代码

/**
 * @date 2025-07-28 8:44
 */
public class CountMaxOrSubsets2044 {

    public int countMaxOrSubsets(int[] nums) {
        int max = 0;
        for (int num : nums) {
            max |= num;
        }
        return dfs(0, 0, nums, max);
    }

    public int dfs(int i, int or, int[] nums, int max) {
        int n = nums.length;
        if (i == n) {
            return 0;
        }
        int cur = or | nums[i];
        return dfs(i + 1, cur, nums, max) + dfs(i + 1, or, nums, max) + (cur == max ? 1 : 0);
    }

}

性能

目标

给你一个整数 n ，按字典序返回范围 [1, n] 内所有整数。

你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。

示例 1：

输入：n = 13
输出：[1,10,11,12,13,2,3,4,5,6,7,8,9]

示例 2：

输入：n = 2
输出：[1,2]

说明：

• 1 <= n <= 5 * 10^4

思路

将 1 ~ n 的所有整数按照字典序排序，要求时间复杂度为 O(n)，空间复杂度为 O(1)。

想象遍历一颗字典树，优先扩展（乘以 10），如果超过 n，则优先将个位数加一（遍历兄弟节点），如果需要进位，则返回父节点（除以10）并将个位数加一（父节点的兄弟节点），接着执行同样的逻辑，扩展，个位数加一，回退。

代码

/**
 * @date 2025-06-08 18:15
 */
public class LexicalOrder386 {

    public List<Integer> lexicalOrder(int n) {
        List<Integer> res = new ArrayList<>();
        for (int i = 0, j = 1; i < n; i++) {
            res.add(j);
            if (j * 10 <= n) {
                j *= 10;
            } else {
                while (j % 10 == 9 || j >= n) {
                    j /= 10;
                }
                j++;
            }
        }
        return res;
    }

}

性能