标签： 脑筋急转弯

目标

给你一个 m x n 的网格图，其中 (0, 0) 是最左上角的格子，(m - 1, n - 1) 是最右下角的格子。给你一个整数数组 startPos ，startPos = [startrow, startcol] 表示 初始 有一个 机器人 在格子 (startrow, startcol) 处。同时给你一个整数数组 homePos ，homePos = [homerow, homecol] 表示机器人的 家 在格子 (homerow, homecol) 处。

机器人需要回家。每一步它可以往四个方向移动：上，下，左，右，同时机器人不能移出边界。每一步移动都有一定代价。再给你两个下标从 0 开始的额整数数组：长度为 m 的数组 rowCosts 和长度为 n 的数组 colCosts 。

• 如果机器人往 上 或者往 下 移动到第 r 行 的格子，那么代价为 rowCosts[r] 。
• 如果机器人往 左 或者往 右 移动到第 c 列 的格子，那么代价为 colCosts[c] 。

请你返回机器人回家需要的 最小总代价 。

示例 1：

输入：startPos = [1, 0], homePos = [2, 3], rowCosts = [5, 4, 3], colCosts = [8, 2, 6, 7]
输出：18
解释：一个最优路径为：
从 (1, 0) 开始
-> 往下走到 (2, 0) 。代价为 rowCosts[2] = 3 。
-> 往右走到 (2, 1) 。代价为 colCosts[1] = 2 。
-> 往右走到 (2, 2) 。代价为 colCosts[2] = 6 。
-> 往右走到 (2, 3) 。代价为 colCosts[3] = 7 。
总代价为 3 + 2 + 6 + 7 = 18

示例 2：

输入：startPos = [0, 0], homePos = [0, 0], rowCosts = [5], colCosts = [26]
输出：0
解释：机器人已经在家了，所以不需要移动。总代价为 0 。

说明：

• m == rowCosts.length
• n == colCosts.length
• 1 <= m, n <= 10^5
• 0 <= rowCosts[r], colCosts[c] <= 10^4
• startPos.length == 2
• homePos.length == 2
• 0 <= startrow, homerow < m
• 0 <= startcol, homecol < n

思路

有一个 m x n 矩阵，其中有一个机器人在坐标 startPos，机器人家的坐标是 homePos，机器人可以上下左右移动，从上/下移动到第 i 行的成本为 rowCosts[i]，从左/右移动到第 j 列的成本为 colCosts[j]，求机器人回家需要的最小总代价。

根据题意代价均为非负数，只要不折返代价就是最小的，可以将横向与纵向移动分开考虑，分别计算 startPos[0] 到 homePos[0] 以及 startPos[1] 到 homePos[1] 的代价。

由于起点与家的相对位置是不确定的，循环的步长(+1 还是 -1)、结束条件(大于等于 还是 小于等于)需要动态定义。

网友题解则是直接减掉了起点的代价，统一由小坐标到大坐标累加成本。

代码

/**
 * @date 2026-04-07 11:21
 */
public class MinCost2087 {

    public int minCost(int[] startPos, int[] homePos, int[] rowCosts, int[] colCosts) {
        int res = 0;
        int sx = startPos[0];
        int sy = startPos[1];
        int hx = homePos[0];
        int hy = homePos[1];
        int dx = sx <= hx ? 1 : -1;
        int dy = sy <= hy ? 1 : -1;
        for (int i = sx + dx; dx == 1 ? i <= hx : i >= hx; i += dx) {
            res += rowCosts[i];
        }
        for (int i = sy + dy; dy == 1 ? i <= hy : i >= hy; i += dy) {
            res += colCosts[i];
        }
        return res;
    }

}

性能

目标

如果一个十进制数字不含任何前导零，且每一位上的数字不是 0 就是 1 ，那么该数字就是一个 十-二进制数 。例如，101 和 1100 都是 十-二进制数，而 112 和 3001 不是。

给你一个表示十进制整数的字符串 n ，返回和为 n 的 十-二进制数 的最少数目。

示例 1：

输入：n = "32"
输出：3
解释：10 + 11 + 11 = 32

示例 2：

输入：n = "82734"
输出：8

示例 3：

输入：n = "27346209830709182346"
输出：9

说明：

• 1 <= n.length <= 10^5
• n 仅由数字组成
• n 不含任何前导零并总是表示正整数

思路

返回整数 n 中的最大数字即可。

代码

/**
 * @date 2026-04-17 16:06
 */
public class MinPartitions1689 {

    public int minPartitions(String n) {
        int res = 0;
        char[] chars = n.toCharArray();
        for (char c : chars) {
            res = Math.max(res, c - '0');
        }
        return res;
    }
}

性能

目标

给你一个 n x n 的整数方阵 matrix 。你可以执行以下操作 任意次 ：

• 选择 matrix 中 相邻 两个元素，并将它们都 乘以 -1 。

如果两个元素有 公共边 ，那么它们就是 相邻 的。

你的目的是 最大化 方阵元素的和。请你在执行以上操作之后，返回方阵的 最大 和。

示例 1：

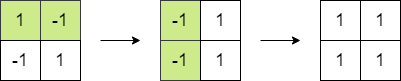
输入：matrix = [[1,-1],[-1,1]]
输出：4
解释：我们可以执行以下操作使和等于 4 ：
- 将第一行的 2 个元素乘以 -1 。
- 将第一列的 2 个元素乘以 -1 。

示例 2：

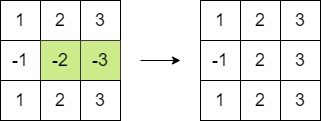
输入：matrix = [[1,2,3],[-1,-2,-3],[1,2,3]]
输出：16
解释：我们可以执行以下操作使和等于 16 ：
- 将第二行的最后 2 个元素乘以 -1 。

说明：

• n == matrix.length == matrix[i].length
• 2 <= n <= 250
• -10^5 <= matrix[i][j] <= 10^5

思路

有一个 n x n 矩阵，每次操作可以将相邻的元素乘以 -1，执行操作任意次，求能够得到的最大方阵和。

经过观察发现，可以将任意两个元素乘以 -1，只需对路径上的每个元素执行操作，改变 (cur, next) 的符号，中间每个元素的符号都被改变了两次，即首尾元素改变了符号。

只需判断矩阵中负数的个数，如果是偶数，可以将负数全部变为相反数；如果是奇数，则需要找到最小的非负数，将其变为负数，其余元素全部变为非负数。

代码

/**
 * @date 2026-01-05 9:07
 */
public class MaxMatrixSum1975 {

    public long maxMatrixSum(int[][] matrix) {
        long res = 0L;
        int negativeCnt = 0;
        int min = Integer.MAX_VALUE;
        for (int[] row : matrix) {
            for (int col : row) {
                res += Math.abs(col);
                min = Math.min(min, Math.abs(col));
                if (col < 0) {
                    negativeCnt++;
                }
            }
        }
        if (negativeCnt % 2 == 1) {
            res -= 2 * min;
        }
        return res;
    }

}

性能

目标

给你一个长度为 n 的数组 complexity。

在房间里有 n 台 上锁的 计算机，这些计算机的编号为 0 到 n - 1，每台计算机都有一个 唯一 的密码。编号为 i 的计算机的密码复杂度为 complexity[i]。

编号为 0 的计算机密码已经 解锁 ，并作为根节点。其他所有计算机必须通过它或其他已经解锁的计算机来解锁，具体规则如下：

• 可以使用编号为 j 的计算机的密码解锁编号为 i 的计算机，其中 j 是任何小于 i 的整数，且满足 complexity[j] < complexity[i]（即 j < i 并且 complexity[j] < complexity[i]）。
• 要解锁编号为 i 的计算机，你需要事先解锁一个编号为 j 的计算机，满足 j < i 并且 complexity[j] < complexity[i]。

求共有多少种 [0, 1, 2, ..., (n - 1)] 的排列方式，能够表示从编号为 0 的计算机（唯一初始解锁的计算机）开始解锁所有计算机的有效顺序。

由于答案可能很大，返回结果需要对 10^9 + 7 取余数。

注意：编号为 0 的计算机的密码已解锁，而 不是 排列中第一个位置的计算机密码已解锁。

排列 是一个数组中所有元素的重新排列。

示例 1：

输入： complexity = [1,2,3]
输出： 2
解释：
有效的排列有：
[0, 1, 2]
首先使用根密码解锁计算机 0。
使用计算机 0 的密码解锁计算机 1，因为 complexity[0] < complexity[1]。
使用计算机 1 的密码解锁计算机 2，因为 complexity[1] < complexity[2]。
[0, 2, 1]
首先使用根密码解锁计算机 0。
使用计算机 0 的密码解锁计算机 2，因为 complexity[0] < complexity[2]。
使用计算机 0 的密码解锁计算机 1，因为 complexity[0] < complexity[1]。

示例 2：

输入： complexity = [3,3,3,4,4,4]
输出： 0
解释：
没有任何排列能够解锁所有计算机。

说明：

• 2 <= complexity.length <= 10^5
• 1 <= complexity[i] <= 10^9

思路

如果要解锁所有计算机，第一台的复杂度必须是唯一最小值。因此可以用第一台解锁后面所有计算机，排列数为 (n - 1)!。

代码

/**
 * @date 2025-12-10 9:06
 */
public class CountPermutations3577 {

    public int countPermutations(int[] complexity) {
        int mod = 1000000007;
        int res = 1;
        int n = complexity.length;
        long c = 1;
        int min = complexity[0];
        for (int i = 1; i < n; i++) {
            if (complexity[i] <= min) {
                return 0;
            }
            res = (int) ((res * c++) % mod);
        }
        return res;
    }

}

性能

目标

在一条无限长的公路上有 n 辆汽车正在行驶。汽车按从左到右的顺序按从 0 到 n - 1 编号，每辆车都在一个 独特的 位置。

给你一个下标从 0 开始的字符串 directions ，长度为 n 。directions[i] 可以是 'L'、'R' 或 'S' 分别表示第 i 辆车是向 左 、向 右 或者 停留 在当前位置。每辆车移动时 速度相同 。

碰撞次数可以按下述方式计算：

• 当两辆移动方向 相反 的车相撞时，碰撞次数加 2 。
• 当一辆移动的车和一辆静止的车相撞时，碰撞次数加 1 。

碰撞发生后，涉及的车辆将无法继续移动并停留在碰撞位置。除此之外，汽车不能改变它们的状态或移动方向。

返回在这条道路上发生的 碰撞总次数 。

示例 1：

输入：directions = "RLRSLL"
输出：5
解释：
将会在道路上发生的碰撞列出如下：
- 车 0 和车 1 会互相碰撞。由于它们按相反方向移动，碰撞数量变为 0 + 2 = 2 。
- 车 2 和车 3 会互相碰撞。由于 3 是静止的，碰撞数量变为 2 + 1 = 3 。
- 车 3 和车 4 会互相碰撞。由于 3 是静止的，碰撞数量变为 3 + 1 = 4 。
- 车 4 和车 5 会互相碰撞。在车 4 和车 3 碰撞之后，车 4 会待在碰撞位置，接着和车 5 碰撞。碰撞数量变为 4 + 1 = 5 。
因此，将会在道路上发生的碰撞总次数是 5 。

示例 2：

输入：directions = "LLRR"
输出：0
解释：
不存在会发生碰撞的车辆。因此，将会在道路上发生的碰撞总次数是 0 。

说明：

• 1 <= directions.length <= 10^5
• directions[i] 的值为 'L'、'R' 或 'S'

思路

无限长的公路上有 n 辆车在行驶，假设公路只有一个车道，directions[i] 表示汽车的行驶方向，L R S 分别表示 左、右、停留三种状态。如果相向而行碰撞次数 +2，装上静止的汽车碰撞次数 +1，发生碰撞后状态均变为停留。返回公路上发生的总碰撞次数。

将行驶方向相同的视为一组，

• 如果当前组行驶方向是 L，并且前面一组是 R，那么碰撞次数为 cntL + cntR，如果前面一组是 S，则碰撞次数为 cntL。
• 如果当前组行驶方向是 S，并且前面一组是 R，那么碰撞次数为 cntR。
• 注意碰撞之后状态变为 S。

代码

/**
 * @date 2025-12-04 9:33
 */
public class CountCollisions2211 {

    public int countCollisions(String directions) {
        int res = 0;
        char[] chars = directions.toCharArray();
        int n = chars.length;
        int i = 0;
        int prevCnt = 0;
        char prev = 'L';
        while (i < n) {
            int start = i;
            while (i < n && chars[i] == chars[start]) {
                i++;
            }
            if (prevCnt != 0) {
                if (chars[start] == 'S' && prev == 'R') {
                    res += prevCnt;
                } else if (chars[start] == 'L' && prev == 'R') {
                    res += prevCnt + i - start;
                    chars[start] = 'S';
                } else if (chars[start] == 'L' && prev == 'S') {
                    res += i - start;
                    chars[start] = 'S';
                }
            }
            prevCnt = i - start;
            prev = chars[start];
        }
        return res;
    }
}

性能

目标

小红和小明在玩一个字符串元音游戏。

给你一个字符串 s，小红和小明将轮流参与游戏，小红 先 开始：

• 在小红的回合，她必须移除 s 中包含 奇数 个元音的任意 非空 子字符串。
• 在小明的回合，他必须移除 s 中包含 偶数 个元音的任意 非空 子字符串。

第一个无法在其回合内进行移除操作的玩家输掉游戏。假设小红和小明都采取 最优策略 。

如果小红赢得游戏，返回 true，否则返回 false。

英文元音字母包括：a, e, i, o, 和 u。

示例 1：

输入： s = "leetcoder"
输出： true
解释：
小红可以执行如下移除操作来赢得游戏：
小红先手，她可以移除加下划线的子字符串 s = "leetcoder"，其中包含 3 个元音。结果字符串为 s = "der"。
小明接着，他可以移除加下划线的子字符串 s = "der"，其中包含 0 个元音。结果字符串为 s = "er"。
小红再次操作，她可以移除整个字符串 s = "er"，其中包含 1 个元音。
又轮到小明，由于字符串为空，无法执行移除操作，因此小红赢得游戏。

示例 2：

输入： s = "bbcd"
输出： false
解释：
小红在她的第一回合无法执行移除操作，因此小红输掉了游戏。

说明：

• 1 <= s.length <= 10^5
• s 仅由小写英文字母组成。

思路

小红与小明在玩字符串元音游戏，小红的回合必须移除包含 奇数 个元音的任意非空子串，小明的回合必须移除包含 偶数 个元音的任意非空子串。如果无法完成操作则输掉游戏，假设小红和小明都采取最优策略，判断小红能否赢得游戏。

如果字符串中包含奇数个元音字符，小红必定获胜。否则，小红应该移除最大的奇数个元音字符，这时剩余一个元音字符，小明只能删除不含元音字符的子串，这时小红将剩余的子串全部删掉，就赢得了游戏。

因此只要字符包含元音字符，小红必定获胜。

代码

/**
 * @date 2025-09-12 8:43
 */
public class DoesAliceWin3227 {

    public boolean doesAliceWin(String s) {
        char[] chars = s.toCharArray();
        for (char c : chars) {
            if (c == 'a' || c == 'e' || c == 'i' || c == 'o' || c == 'u') {
                return true;
            }
        }
        return false;
    }
}

性能

目标

给你两个整数：num1 和 num2 。

在一步操作中，你需要从范围 [0, 60] 中选出一个整数 i ，并从 num1 减去 2^i + num2 。

请你计算，要想使 num1 等于 0 需要执行的最少操作数，并以整数形式返回。

如果无法使 num1 等于 0 ，返回 -1 。

示例 1：

输入：num1 = 3, num2 = -2
输出：3
解释：可以执行下述步骤使 3 等于 0 ：
- 选择 i = 2 ，并从 3 减去 2^2 + (-2) ，num1 = 3 - (4 + (-2)) = 1 。
- 选择 i = 2 ，并从 1 减去 2^2 + (-2) ，num1 = 1 - (4 + (-2)) = -1 。
- 选择 i = 0 ，并从 -1 减去 2^0 + (-2) ，num1 = (-1) - (1 + (-2)) = 0 。
可以证明 3 是需要执行的最少操作数。

示例 2：

输入：num1 = 5, num2 = 7
输出：-1
解释：可以证明，执行操作无法使 5 等于 0 。

说明：

• 1 <= num1 <= 10^9
• -10^9 <= num2 <= 10^9

思路

已知整数 num1 和 num2，每次操作需要从 0 ~ 60 选一个整数 i，并将 num1 -= 2^i + num2，返回将 num1 变为 0 的最小操作次数，如果无法完成返回 -1。

假设最少需要操作 k 次，那么 num1 - k * num2 = 2^i1 + 2^i2 + …… + 2^ik，其中 ik 表示第 k 次选择的 i。

问题转换为 num1 - k * num2 能否用 k 个 2 的幂表示。

二进制中 1 的个数就是最少的 k 的个数，它自身的值就是最多可以拆分的个数 ，也就是说 num = num1 - k * num2 的二进制表示中 1 的个数应小于等于 k 并且 num >= k。

代码

/**
 * @date 2025-09-05 8:46
 */
public class MakeTheIntegerZero2749 {

    public int makeTheIntegerZero(int num1, int num2) {
        for (int i = 0; i < 61; i++) {
            long num = num1 - (long) i * num2;
            if (num <= 0) {
                return -1;
            } else if (Long.bitCount(num) <= i && num >= i) {
                return i;
            }
        }
        return -1;
    }

}

性能

目标

给你一个长度为 n 的整数数组 nums 。

考虑 nums 中进行 按位与（bitwise AND）运算得到的值 最大 的 非空 子数组。

• 换句话说，令 k 是 nums 任意 子数组执行按位与运算所能得到的最大值。那么，只需要考虑那些执行一次按位与运算后等于 k 的子数组。

返回满足要求的 最长 子数组的长度。

数组的按位与就是对数组中的所有数字进行按位与运算。

子数组 是数组中的一个连续元素序列。

示例 1：

输入：nums = [1,2,3,3,2,2]
输出：2
解释：
子数组按位与运算的最大值是 3 。
能得到此结果的最长子数组是 [3,3]，所以返回 2 。

示例 2：

输入：nums = [1,2,3,4]
输出：1
解释：
子数组按位与运算的最大值是 4 。
能得到此结果的最长子数组是 [4]，所以返回 1 。

说明：

• 1 <= nums.length <= 10^5
• 1 <= nums[i] <= 10^6

思路

两个数按位与的结果一定不会比这两个数更大。问题转化为连续的最大值长度。

代码

/**
 * @date 2025-07-30 10:28
 */
public class LongestSubarray2419 {

    public int longestSubarray(int[] nums) {
        int n = nums.length;
        int max = Arrays.stream(nums).max().getAsInt();
        int res = 1;
        int i = 0;
        while (i < n){
            int l = 0;
            while (i < n && nums[i++] == max){
                l++;
            }
            res = Math.max(res, l);
        }
        return res;
    }
}

性能