目标
给你一个下标从 0 开始的二进制数组 nums,其长度为 n ;另给你一个 正整数 k 以及一个 非负整数 maxChanges 。
Alice 在玩一个游戏,游戏的目标是让 Alice 使用 最少 数量的 行动 次数从 nums 中拾起 k 个 1 。游戏开始时,Alice 可以选择数组 [0, n - 1] 范围内的任何索引 aliceIndex 站立。如果 nums[aliceIndex] == 1 ,Alice 会拾起一个 1 ,并且 nums[aliceIndex] 变成0(这 不算 作一次行动)。之后,Alice 可以执行 任意数量 的 行动(包括零次),在每次行动中 Alice 必须 恰好 执行以下动作之一:
- 选择任意一个下标 j != aliceIndex 且满足 nums[j] == 0 ,然后将 nums[j] 设置为 1 。这个动作最多可以执行 maxChanges 次。
- 选择任意两个相邻的下标 x 和 y(|x - y| == 1)且满足 nums[x] == 1, nums[y] == 0 ,然后交换它们的值(将 nums[y] = 1 和 nums[x] = 0)。如果 y == aliceIndex,在这次行动后 Alice 拾起一个 1 ,并且 nums[y] 变成 0 。
返回 Alice 拾起 恰好 k 个 1 所需的 最少 行动次数。
示例 1:
输入:nums = [1,1,0,0,0,1,1,0,0,1], k = 3, maxChanges = 1
输出:3
解释:如果游戏开始时 Alice 在 aliceIndex == 1 的位置上,按照以下步骤执行每个动作,他可以利用 3 次行动拾取 3 个 1 :
游戏开始时 Alice 拾取了一个 1 ,nums[1] 变成了 0。此时 nums 变为 [1,0,0,0,0,1,1,0,0,1] 。
选择 j == 2 并执行第一种类型的动作。nums 变为 [1,0,1,0,0,1,1,0,0,1]
选择 x == 2 和 y == 1 ,并执行第二种类型的动作。nums 变为 [1,1,0,0,0,1,1,0,0,1] 。由于 y == aliceIndex,Alice 拾取了一个 1 ,nums 变为 [1,0,0,0,0,1,1,0,0,1] 。
选择 x == 0 和 y == 1 ,并执行第二种类型的动作。nums 变为 [0,1,0,0,0,1,1,0,0,1] 。由于 y == aliceIndex,Alice 拾取了一个 1 ,nums 变为 [0,0,0,0,0,1,1,0,0,1] 。
请注意,Alice 也可能执行其他的 3 次行动序列达成拾取 3 个 1 。
示例 2:
输入:nums = [0,0,0,0], k = 2, maxChanges = 3
输出:4
解释:如果游戏开始时 Alice 在 aliceIndex == 0 的位置上,按照以下步骤执行每个动作,他可以利用 4 次行动拾取 2 个 1 :
选择 j == 1 并执行第一种类型的动作。nums 变为 [0,1,0,0] 。
选择 x == 1 和 y == 0 ,并执行第二种类型的动作。nums 变为 [1,0,0,0] 。由于 y == aliceIndex,Alice 拾起了一个 1 ,nums 变为 [0,0,0,0] 。
再次选择 j == 1 并执行第一种类型的动作。nums 变为 [0,1,0,0] 。
再次选择 x == 1 和 y == 0 ,并执行第二种类型的动作。nums 变为 [1,0,0,0] 。由于y == aliceIndex,Alice 拾起了一个 1 ,nums 变为 [0,0,0,0] 。
说明:
- 2 <= n <= 10^5
- 0 <= nums[i] <= 1
- 1 <= k <= 10^5
- 0 <= maxChanges <= 10^5
- maxChanges + sum(nums) >= k
思路
有一个二进制(元素不是0就是1)数组nums,选择一个固定的位置aliceIndex,如果该位置元素值为1,则可以拾起并将元素置0。接下来可以采取行动:
- 任选一个不等于aliceIndex且值为0的元素置1
- 将任意相邻且元素值不等的元素交换,如果其中一个位置是aliceIndex,且交换后的值为1,则可以拾起这个1并将元素置0
问恰好拾起k个1所需最小行动次数。
很明显行动1要选与aliceIndex相邻的,这样才可以用行动2将1拾起。
我们首先面对的问题是aliceIndex怎么选,要拾取1就需要将1都通过行动2移动到aliceIndex周围,如果拾取一个1的行动次数大于2的话就需要考虑使用行动1直接在aliceIndex周围设置1再拾取。
// todo
代码
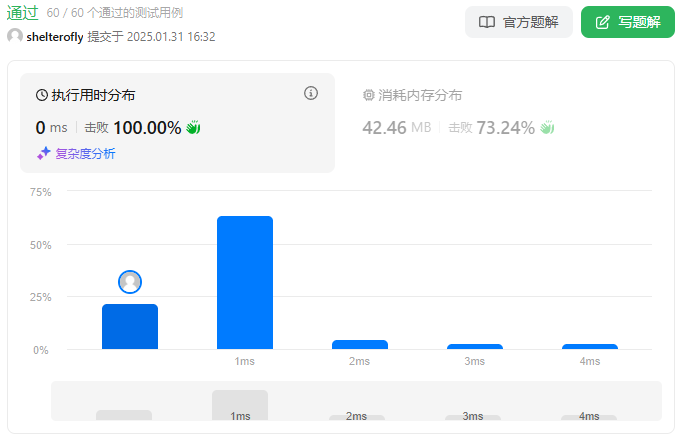
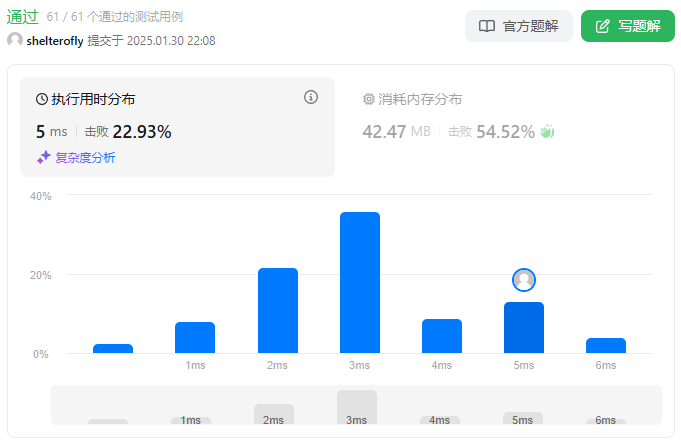
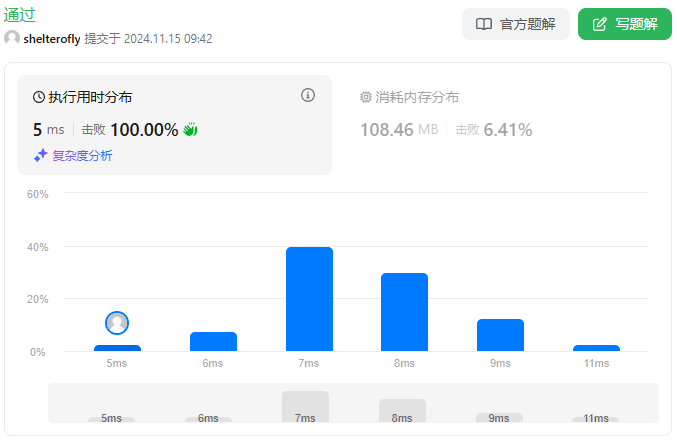
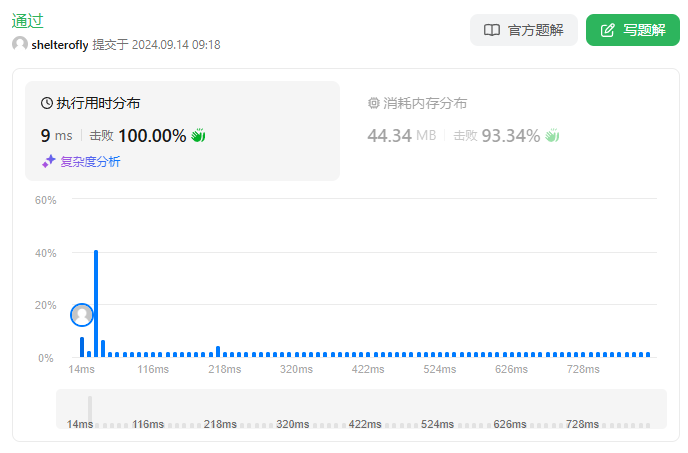
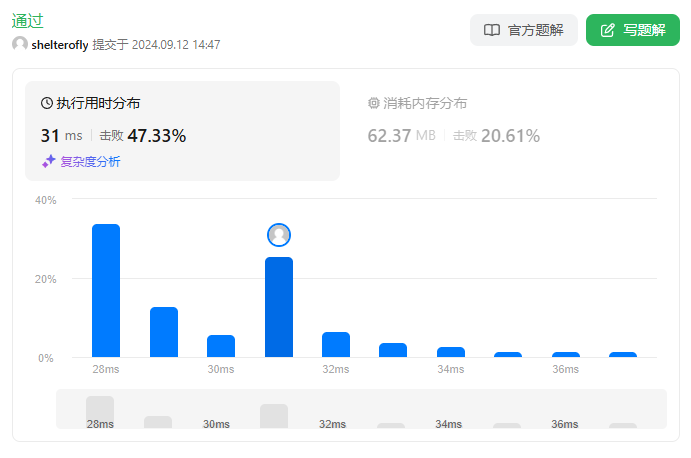
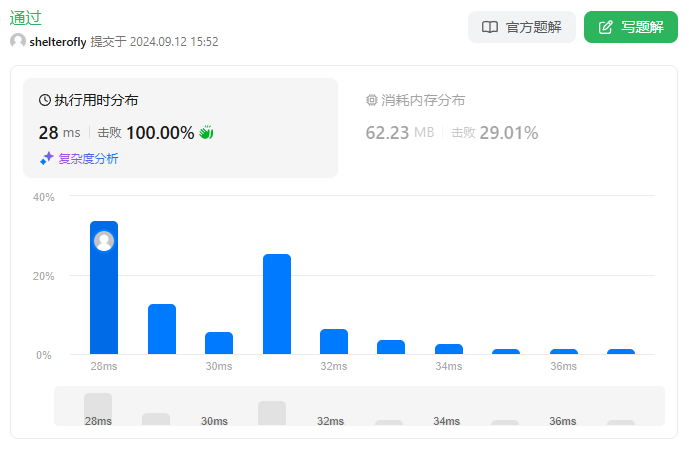
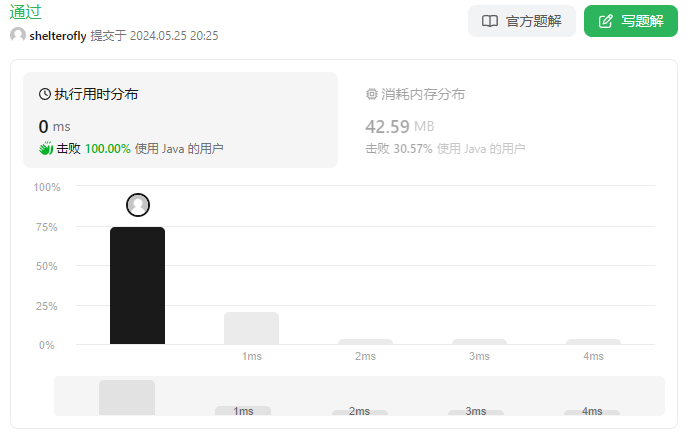
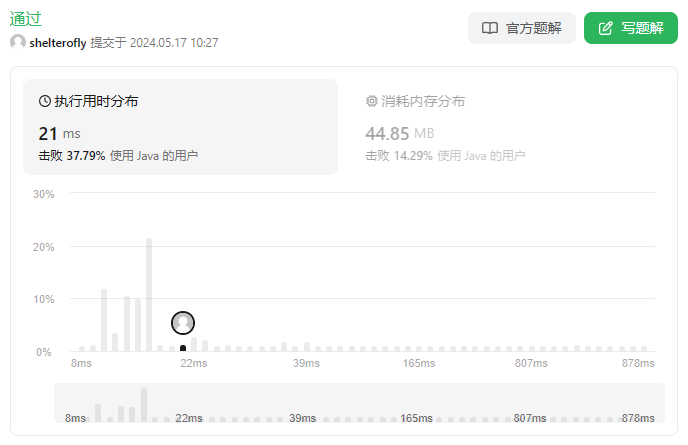
性能