标签： 动态规划

63.不同路径II

目标

给定一个 m x n 的整数数组 grid。一个机器人初始位于 左上角（即 grid[0][0]）。机器人尝试移动到 右下角（即 grid[m - 1][n - 1]）。机器人每次只能向下或者向右移动一步。

网格中的障碍物和空位置分别用 1 和 0 来表示。机器人的移动路径中不能包含 任何 有障碍物的方格。

返回机器人能够到达右下角的不同路径数量。

测试用例保证答案小于等于 2 * 109。

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

说明：

  • m == obstacleGrid.length
  • n == obstacleGrid[i].length
  • 1 <= m, n <= 100
  • obstacleGrid[i][j] 为 0 或 1

思路

有一个 m x n 的二进制矩阵，0 代表空位，1 代表有障碍物。有一个机器人可以向右或向下移动，求从 (0,0) 到 (m - 1, n - 1) 的路径有多少。

定义 dp[i][j] 表示到达坐标 (i - 1, j - 1) 的不同路径数。这样定义可以省去单独初始化第一行第一列。状态转移方程为 当 obstacleGrid[i][j] == 0 时, dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，初值为 dp[0][1] = 1，可以视为从 (-1, 0) 到 (0, 0) 的路径数量，如果 (0, 0) 有障碍物则为 0，否则为 1。

代码


/**
 * @date 2025-02-01 20:05
 */
public class UniquePathsWithObstacles63 {

     public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][] dp = new int[m + 1][n + 1];
        dp[0][1] = 1;
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (obstacleGrid[i - 1][j - 1] == 0){
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                }
            }
        }
        return dp[m][n];
    }

}

性能

45.跳跃游戏II

目标

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向后跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

  • 0 <= j <= nums[i]
  • i + j < n

返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

说明:

  • 1 <= nums.length <= 10^4
  • 0 <= nums[i] <= 1000
  • 题目保证可以到达 nums[n-1]

思路

数组 nums 的元素表示可以向后跳跃的最大长度，求从 0 跳到 n - 1 所需的最小跳跃次数。

定义 dp[i] 表示到达下标 i 所需的最小跳跃次数，状态转移方程为 dp[i + k] = min(dp[i] + 1)，其中 k ∈ [1, nums[i]]。

代码


/**
 * @date 2024-03-07 17:14
 */
public class CanJumpII45 {

    public int jump(int[] nums) {
        int n = nums.length;
        int[] dp = new int[n];
        Arrays.fill(dp, 0x3f3f3f);
        dp[0] = 0;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n && j <= i + nums[i]; j++) {
                dp[j] = Math.min(dp[j], dp[i] + 1);
            }
        }
        return dp[n - 1];
    }

}

性能

2944.购买水果需要的最少金币数

目标

给你一个 下标从 1 开始的 整数数组 prices ，其中 prices[i] 表示你购买第 i 个水果需要花费的金币数目。

水果超市有如下促销活动：

  • 如果你花费 prices[i] 购买了下标为 i 的水果，那么你可以免费获得下标范围在 [i + 1, i + i + 1] 的水果。

注意 ，即使你 可以 免费获得水果 j ，你仍然可以花费 prices[j] 个金币去购买它以获得它的奖励。

请你返回获得所有水果所需要的 最少 金币数。

示例 1：

输入：prices = [3,1,2]
输出：4
解释：
用 prices[0] = 3 个金币购买第 1 个水果，你可以免费获得第 2 个水果。
用 prices[1] = 1 个金币购买第 2 个水果，你可以免费获得第 3 个水果。
免费获得第 3 个水果。
请注意，即使您可以免费获得第 2 个水果作为购买第 1 个水果的奖励，但您购买它是为了获得其奖励，这是更优化的。

示例 2：

输入：prices = [1,10,1,1]
输出：2
解释：
用 prices[0] = 1 个金币购买第 1 个水果，你可以免费获得第 2 个水果。
免费获得第 2 个水果。
用 prices[2] = 1 个金币购买第 3 个水果，你可以免费获得第 4 个水果。
免费获得第 4 个水果。

示例 3：

输入：prices = [26,18,6,12,49,7,45,45]
输出：39
解释：
用 prices[0] = 26 个金币购买第 1 个水果，你可以免费获得第 2 个水果。
免费获得第 2 个水果。
用 prices[2] = 6 个金币购买第 3 个水果，你可以免费获得第 4，5，6（接下来的三个）水果。
免费获得第 4 个水果。
免费获得第 5 个水果。
用 prices[5] = 7 个金币购买第 6 个水果，你可以免费获得第 7 和 第 8 个水果。
免费获得第 7 个水果。
免费获得第 8 个水果。
请注意，即使您可以免费获得第 6 个水果作为购买第 3 个水果的奖励，但您购买它是为了获得其奖励，这是更优化的。

说明：

1 <= prices.length <= 1000
1 <= prices[i] <= 10^5

思路

有 n 个水果，其价格由 prices 表示，当我们以 prices[i] 枚金币购买了第 i + 1 个苹果时，我们可以免费获得下标 [i + 1, i + i + 1] 的 所有 个苹果（当然也可以购买以获得后面的奖励），求获得全部苹果所需的最少硬币。

最直接的想法是记忆化搜索。

代码


/**
 * @date 2025-01-24 9:07
 */
public class MinimumCoins2944 {

    public int minimumCoins(int[] prices) {
        int[] mem = new int[2 * prices.length + 3];
        Arrays.fill(mem, Integer.MAX_VALUE);
        return dfs(0, prices, mem, 0);
    }

    public int dfs(int index, int[] prices, int[] mem, int cost) {
        int n = prices.length;
        if (index >= n) {
            return cost;
        }
        int res = cost + prices[index];
        int next = index * 2 + 2;
        if (mem[next] == Integer.MAX_VALUE) {
            mem[next] = dfs(next, prices, mem, 0);
        }
        int remainder = mem[next];
        if (remainder == 0) {
            return res;
        }
        for (int i = index + 1; i < n && i <= index * 2 + 1; i++) {
            if (mem[i] == Integer.MAX_VALUE) {
                mem[i] = dfs(i, prices, mem, 0);
            }
            remainder = Math.min(mem[i], remainder);
        }
        return res + remainder;
    }

}

性能

2920.收集所有金币可获得的最大积分

目标

有一棵由 n 个节点组成的无向树，以 0 为根节点，节点编号从 0 到 n - 1 。给你一个长度为 n - 1 的二维 整数 数组 edges ，其中 edges[i] = [ai, bi] 表示在树上的节点 ai 和 bi 之间存在一条边。另给你一个下标从 0 开始、长度为 n 的数组 coins 和一个整数 k ，其中 coins[i] 表示节点 i 处的金币数量。

从根节点开始，你必须收集所有金币。要想收集节点上的金币，必须先收集该节点的祖先节点上的金币。

节点 i 上的金币可以用下述方法之一进行收集：

  • 收集所有金币，得到共计 coins[i] - k 点积分。如果 coins[i] - k 是负数，你将会失去 abs(coins[i] - k) 点积分。
  • 收集所有金币，得到共计 floor(coins[i] / 2) 点积分。如果采用这种方法，节点 i 子树中所有节点 j 的金币数 coins[j] 将会减少至 floor(coins[j] / 2) 。

返回收集 所有 树节点的金币之后可以获得的最大积分。

示例 1：

输入：edges = [[0,1],[1,2],[2,3]], coins = [10,10,3,3], k = 5
输出：11
解释：
使用第一种方法收集节点 0 上的所有金币。总积分 = 10 - 5 = 5 。
使用第一种方法收集节点 1 上的所有金币。总积分 = 5 + (10 - 5) = 10 。
使用第二种方法收集节点 2 上的所有金币。所以节点 3 上的金币将会变为 floor(3 / 2) = 1 ，总积分 = 10 + floor(3 / 2) = 11 。
使用第二种方法收集节点 3 上的所有金币。总积分 =  11 + floor(1 / 2) = 11.
可以证明收集所有节点上的金币能获得的最大积分是 11 。

示例 2：

输入：edges = [[0,1],[0,2]], coins = [8,4,4], k = 0
输出：16
解释：
使用第一种方法收集所有节点上的金币，因此，总积分 = (8 - 0) + (4 - 0) + (4 - 0) = 16 。

说明：

  • n == coins.length
  • 2 <= n <= 10^5
  • 0 <= coins[i] <= 10^4
  • edges.length == n - 1
  • 0 <= edges[i][0], edges[i][1] < n
  • 0 <= k <= 10^4

提示：

  • Let dp[x][t] be the maximum points we can get from the subtree rooted at node x and the second operation has been used t times in its ancestors.
  • Note that the value of each node <= 104, so when t >= 14 dp[x][t] is always 0.
  • General equation will be: dp[x][t] = max((coins[x] >> t) - k + sigma(dp[y][t]), (coins[x] >> (t + 1)) + sigma(dp[y][t + 1])) where nodes denoted by y in the sigma, are the direct children of node x.

思路

定义 dp[x][t] 表示 x 的祖先节点已经使用了 t 次方法二，当前节点及其子树所能获得的最大积分，最终结果为 dp[0][0]。状态转移方程为 dp[x][t] = Math.max(Σdp[c][t] + (coins[x] >> t) - k, Σdp[c][t + 1] + (coins[x] >> (t + 1)))，其中 c 是当前节点的直接孩子节点。

代码


/**
 * @date 2025-01-23 10:20
 */
public class MaximumPoints2920 {

    public int maximumPoints(int[][] edges, int[] coins, int k) {
        int n = coins.length;
        // 建图
        List<Integer>[] g = new ArrayList[n];
        for (int i = 0; i < n; i++) {
            g[i] = new ArrayList<>();
        }
        for (int[] edge : edges) {
            int from = edge[0];
            int to = edge[1];
            g[from].add(to);
            g[to].add(from);
        }
        // bfs 获得层级结构
        List<List<Integer>> depthNodes = new ArrayList<>();
        List<Integer> l = new ArrayList<>();
        l.add(0);
        depthNodes.add(l);
        Queue<Integer> q = new ArrayDeque<>();
        q.offer(0);
        while (!q.isEmpty()) {
            int size = q.size();
            List<Integer> list = new ArrayList<>();
            for (int i = 0; i < size; i++) {
                Integer from = q.poll();
                for (Integer to : g[from]) {
                    list.add(to);
                    g[to].removeIf(next -> next.equals(from));
                }
            }
            if (list.size() > 0) {
                depthNodes.add(list);
                q.addAll(list);
            }
        }
        // 初始化叶子节点的分数
        int[][] dp = new int[n][15];
        int depth = depthNodes.size();
        for (Integer leaf : depthNodes.get(depth - 1)) {
            for (int t = 0; t < 14; t++) {
                dp[leaf][t] = Math.max((coins[leaf] >> t) - k, (coins[leaf] >> (t + 1)));
            }
        }
        // 自底向上计算子树分数和的最大值
        for (int d = depth - 2; d >= 0; d--) {
            List<Integer> nodes = depthNodes.get(d);
            for (Integer cur : nodes) {
                for (int t = 0; t < 14; t++) {
                    int sum0 = 0;
                    int sum1 = 0;
                    for (Integer child : g[cur]) {
                        sum0 += dp[child][t];
                        sum1 += dp[child][t + 1];
                    }
                    dp[cur][t] = Math.max(sum0 + (coins[cur] >> t) - k, sum1 + (coins[cur] >> (t + 1)));
                }
            }
        }
        return dp[0][0];
    }

}

性能

2218.从栈中取出K个硬币的最大面值和

目标

一张桌子上总共有 n 个硬币 栈 。每个栈有 正整数 个带面值的硬币。

每一次操作中，你可以从任意一个栈的 顶部 取出 1 个硬币，从栈中移除它，并放入你的钱包里。

给你一个列表 piles ，其中 piles[i] 是一个整数数组，分别表示第 i 个栈里 从顶到底 的硬币面值。同时给你一个正整数 k ，请你返回在 恰好 进行 k 次操作的前提下，你钱包里硬币面值之和 最大为多少 。

示例 1：

输入：piles = [[1,100,3],[7,8,9]], k = 2
输出：101
解释：
上图展示了几种选择 k 个硬币的不同方法。
我们可以得到的最大面值为 101 。

示例 2：

输入：piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7
输出：706
解释：
如果我们所有硬币都从最后一个栈中取，可以得到最大面值和。

说明：

  • n == piles.length
  • 1 <= n <= 1000
  • 1 <= piles[i][j] <= 10^5
  • 1 <= k <= sum(piles[i].length) <= 2000

思路

有 n 个栈，栈中有 piles[i].length 个硬币，每次操作可以从任意栈顶取一个硬币，求 k 次操作取得的硬币和的最大值。

定义 dp[i][j] 表示 从前 i + 1 个栈中最多取 j 个 所能得到的最大值，与 0 - 1 背包不同的是我们需要枚举从当前栈取 1 至 x 枚硬币的最大值，状态转移方程为 dp[i][j] = Math.max(dp[i][j], Math.max(dp[i - 1][j], dp[i - 1][j - x] + prefix[i][x]))，外层 max 求的是当前栈每种取法的最大值，第二个参数的 max 求的是当前栈 不取 或者 取 x 枚硬币对应的最大值。由于是从栈顶取，我们使用前缀和 prefix 记录每个栈从栈顶到底的硬币和。

代码


/**
 * @date 2025-01-21 13:46
 */
public class MaxValueOfCoins2218 {

    public int maxValueOfCoins(List<List<Integer>> piles, int k) {
        int n = piles.size();
        int[][] prefix = new int[n][];
        // 计算前缀和
        for (int i = 0; i < n; i++) {
            List<Integer> pile = piles.get(i);
            prefix[i] = new int[pile.size() + 1];
            for (int j = 1; j <= pile.size(); j++) {
                prefix[i][j] = prefix[i][j - 1] + pile.get(j - 1);
            }
        }
        // 定义dp[i][j] 表示 从前 i + 1 个栈中最多取 j 个 所能得到的最大值
        int[][] dp = new int[n][k + 1];
        // 初始化，从第一个栈最多取 k 个
        for (int j = 1; j <= k; j++) {
            int length = piles.get(0).size();
            if (j <= length) {
                dp[0][j] = prefix[0][j];
            } else {
                dp[0][j] = dp[0][length];
            }
        }
        for (int i = 1; i < n; i++) {
            // 枚举右边界
            int length = piles.get(i).size();
            for (int j = 1; j <= k; j++) {
                // j 表示从前 i + 1 个栈中总共取 j 个
                for (int x = 1; x <= length && j >= x; x++) {
                    // 表示从当前栈中取 x 个
                    dp[i][j] = Math.max(dp[i][j], Math.max(dp[i - 1][j], dp[i - 1][j - x] + prefix[i][x]));
                }
            }
        }
        return dp[n - 1][k];
    }

}

性能

2266.统计打字方案数

目标

Alice 在给 Bob 用手机打字。数字到字母的 对应 如下图所示。

为了 打出 一个字母，Alice 需要 按 对应字母 i 次，i 是该字母在这个按键上所处的位置。

  • 比方说，为了按出字母 's' ，Alice 需要按 '7' 四次。类似的， Alice 需要按 '5' 两次得到字母 'k' 。
  • 注意，数字 '0' 和 '1' 不映射到任何字母，所以 Alice 不 使用它们。

但是，由于传输的错误，Bob 没有收到 Alice 打字的字母信息，反而收到了 按键的字符串信息 。

  • 比方说，Alice 发出的信息为 "bob" ，Bob 将收到字符串 "2266622" 。

给你一个字符串 pressedKeys ，表示 Bob 收到的字符串，请你返回 Alice 总共可能发出多少种文字信息 。

由于答案可能很大，将它对 10^9 + 7 取余 后返回。

示例 1：

输入：pressedKeys = "22233"
输出：8
解释：
Alice 可能发出的文字信息包括：
"aaadd", "abdd", "badd", "cdd", "aaae", "abe", "bae" 和 "ce" 。
由于总共有 8 种可能的信息，所以我们返回 8 。

示例 2：

输入：pressedKeys = "222222222222222222222222222222222222"
输出：82876089
解释：
总共有 2082876103 种 Alice 可能发出的文字信息。
由于我们需要将答案对 109 + 7 取余，所以我们返回 2082876103 % (109 + 7) = 82876089 。

说明：

  • 1 <= pressedKeys.length <= 10^5
  • pressedKeys 只包含数字 '2' 到 '9' 。

思路

Alice 给 Bob 发短信，由于种种原因，Bob 接收到的是 Alice 的按键的数字字符串，求这些按键信息能够表示多少文字信息。由于一个数字按键可以表示多个字母，那么连续的相同数字就产生了多种可能的文字信息。2 3 4 5 6 8 可以表示 3 个字母，7 9 可以表示 4 个字母。

问题变成求解相同的连续数字可以表示的字母组合个数，或者将 n 个球放入盒子，每个盒子最多放 k 个球，至少放 1 个球，有多少种放法。

定义 dp[i] 表示将 i 个球放入盒子的方法，考虑最后一个盒子我们可以放 1 ~ k 个球，那么当 k = 3 或 k = 4 时：

  • dp3[i] = ((dp3[i - 1] + dp3[i - 2]) % MOD + dp3[i - 3] % MOD) % MOD;
  • dp4[i] = ((dp4[i - 1] + dp4[i - 2]) % MOD + (dp4[i - 3] + dp4[i - 4]) % MOD) % MOD;

遍历字符串，找到连续的字符个数，使用乘法原理计算即可。

代码


/**
 * @date 2025-01-19 2:21
 */
public class CountTexts2266 {

    static int[] dp3 = new int[100001];
    static int[] dp4 = new int[100001];
    static int MOD = 1000000007;
    static Map<Character, int[]> map = new HashMap<>();

    static {
        dp3[1] = 1;
        dp3[2] = 2;
        dp3[3] = 4;
        dp3[4] = 7;
        dp4[1] = 1;
        dp4[2] = 2;
        dp4[3] = 4;
        dp4[4] = 8;
        for (int i = 5; i < 100001; i++) {
            dp3[i] = ((dp3[i - 1] + dp3[i - 2]) % MOD + dp3[i - 3] % MOD) % MOD;
            dp4[i] = ((dp4[i - 1] + dp4[i - 2]) % MOD + (dp4[i - 3] + dp4[i - 4]) % MOD) % MOD;
        }
        map.put('2', dp3);
        map.put('3', dp3);
        map.put('4', dp3);
        map.put('5', dp3);
        map.put('6', dp3);
        map.put('8', dp3);
        map.put('7', dp4);
        map.put('9', dp4);
    }

    public int countTexts(String pressedKeys) {
        char[] chars = pressedKeys.toCharArray();
        char prev = chars[0];
        int cnt = 1;
        long res = 1;
        for (int i = 1; i < chars.length; i++) {
            if (prev == chars[i]) {
                cnt++;
            } else {
                res = res * map.get(prev)[cnt] % MOD;
                prev = chars[i];
                cnt = 1;
            }
        }
        if (cnt > 1){
            res = res * map.get(prev)[cnt] % MOD;
        }
        return (int) res;
    }

}

性能

3287.求出数组中最大序列值

目标

给你一个整数数组 nums 和一个 正 整数 k 。

定义长度为 2 * x 的序列 seq 的 值 为：

  • (seq[0] OR seq[1] OR ... OR seq[x - 1]) XOR (seq[x] OR seq[x + 1] OR ... OR seq[2 * x - 1]).

请你求出 nums 中所有长度为 2 * k 的 子序列 的 最大值 。

示例 1：

输入：nums = [2,6,7], k = 1
输出：5
解释：
子序列 [2, 7] 的值最大，为 2 XOR 7 = 5 。

示例 2：

输入：nums = [4,2,5,6,7], k = 2
输出：2
解释：
子序列 [4, 5, 6, 7] 的值最大，为 (4 OR 5) XOR (6 OR 7) = 2 。

说明：

  • 2 <= nums.length <= 400
  • 1 <= nums[i] < 27
  • 1 <= k <= nums.length / 2

思路

// todo

代码

性能

1387.将整数按权重排序

目标

我们将整数 x 的 权重 定义为按照下述规则将 x 变成 1 所需要的步数：

  • 如果 x 是偶数，那么 x = x / 2
  • 如果 x 是奇数，那么 x = 3 * x + 1

比方说，x=3 的权重为 7 。因为 3 需要 7 步变成 1 （3 --> 10 --> 5 --> 16 --> 8 --> 4 --> 2 --> 1）。

给你三个整数 lo， hi 和 k 。你的任务是将区间 [lo, hi] 之间的整数按照它们的权重 升序排序 ，如果大于等于 2 个整数有 相同 的权重，那么按照数字自身的数值 升序排序 。

请你返回区间 [lo, hi] 之间的整数按权重排序后的第 k 个数。

注意，题目保证对于任意整数 x （lo <= x <= hi） ，它变成 1 所需要的步数是一个 32 位有符号整数。

示例 1：

输入：lo = 12, hi = 15, k = 2
输出：13
解释：12 的权重为 9（12 --> 6 --> 3 --> 10 --> 5 --> 16 --> 8 --> 4 --> 2 --> 1）
13 的权重为 9
14 的权重为 17
15 的权重为 17
区间内的数按权重排序以后的结果为 [12,13,14,15] 。对于 k = 2 ，答案是第二个整数也就是 13 。
注意，12 和 13 有相同的权重，所以我们按照它们本身升序排序。14 和 15 同理。

示例 2：

输入：lo = 7, hi = 11, k = 4
输出：7
解释：区间内整数 [7, 8, 9, 10, 11] 对应的权重为 [16, 3, 19, 6, 14] 。
按权重排序后得到的结果为 [8, 10, 11, 7, 9] 。
排序后数组中第 4 个数字为 7 。

说明：

1 <= lo <= hi <= 1000
1 <= k <= hi - lo + 1

思路

定义整数 x 的权重为 将其变为 1 的操作次数，根据整数的奇偶性，可以执行不同的操作：

  • x 为偶数，x -> x / 2
  • x 为奇数，x -> 3 * x + 1

返回区间 [lo, hi] 之间的整数按权重排序后的第 k 个数。

根据题意模拟计算出每个数字的权重，将它和数字一起保存起来，然后按照权重、数值排序即可。

可以预处理 1 ~ 1000 内的所有权重，保存中间结果减少重复计算。

看到题目时我们都会有这样的疑问，如何证明 x 最终都会回到 1？有网友提到题目中的操作与考拉兹猜想（Collatz conjecture）的操作一样，由于操作过程与冰雹的形成和下落过程相似，因此也叫冰雹猜想。

代码


/**
 * @date 2024-12-22 16:20
 */
public class GetKth1387 {

    public int getKth(int lo, int hi, int k) {
        int n = hi - lo + 1;
        int[][] w = new int[n][2];
        int c = 0;
        for (int i = lo; i <= hi; i++) {
            w[c++] = new int[]{getWeight(i), i};
        }
        Arrays.sort(w, (a, b) -> {
            int compare = a[0] - b[0];
            if (compare != 0) {
                return compare;
            }
            return a[1] - b[1];
        });
        return w[k - 1][1];
    }

    public int getWeight(int x) {
        int cnt = 0;
        while (x > 1) {
            if (x % 2 == 0) {
                x >>= 1;
            } else {
                x = 3 * x + 1;
            }
            cnt++;
        }
        return cnt;
    }
}

性能

3291.形成目标字符串需要的最少字符串数I

目标

给你一个字符串数组 words 和一个字符串 target。

如果字符串 x 是 words 中 任意 字符串的 前缀，则认为 x 是一个 有效 字符串。

现计划通过 连接 有效字符串形成 target ，请你计算并返回需要连接的 最少 字符串数量。如果无法通过这种方式形成 target，则返回 -1。

示例 1：

输入： words = ["abc","aaaaa","bcdef"], target = "aabcdabc"
输出： 3
解释：
target 字符串可以通过连接以下有效字符串形成：
words[1] 的长度为 2 的前缀，即 "aa"。
words[2] 的长度为 3 的前缀，即 "bcd"。
words[0] 的长度为 3 的前缀，即 "abc"。

示例 2：

输入： words = ["abababab","ab"], target = "ababaababa"
输出： 2
解释：
target 字符串可以通过连接以下有效字符串形成：
words[0] 的长度为 5 的前缀，即 "ababa"。
words[0] 的长度为 5 的前缀，即 "ababa"。

示例 3：

输入： words = ["abcdef"], target = "xyz"
输出： -1

说明：

  • 1 <= words.length <= 100
  • 1 <= words[i].length <= 5 * 10^3
  • 输入确保 sum(words[i].length) <= 10^5。
  • words[i] 只包含小写英文字母。
  • 1 <= target.length <= 5 * 10^3
  • target 只包含小写英文字母。

思路

有一个字符串数组 words 和目标字符串 target，请你使用最少的字符串前缀组成 target，返回需要的字符串数量，如果无法组成 target 返回 -1。

注意前缀是允许重复使用的，状态个数为 target.length ^ 2，深度为 100，直接使用记忆化搜索会超时。

使用字典树加动态规划可以勉强通过，但是明天的通过不了。

//todo KMP 算法 Z 函数 / 字符串哈希+二分 / AC 自动机

代码


/**
 * @date 2024-12-17 8:59
 */
public class MinValidStrings3291 {

    static public class Trie {
        public boolean isLeaf;
        public Trie[] children;

        public Trie() {
            this.children = new Trie[26];
        }

        public Trie build(String[] dict) {
            Trie root = this;
            for (String word : dict) {
                root = this;
                char[] chars = word.toCharArray();
                for (int i = 0; i < chars.length; i++) {
                    int c = chars[i] - 'a';
                    if (root.children[c] == null) {
                        root.children[c] = new Trie();
                    }
                    root = root.children[c];
                }
                root.isLeaf = true;
            }
            return root;
        }

        public int exists(char[] target, int start) {
            int n = target.length;
            int length = 0;
            Trie root = this;
            int c = target[start] - 'a';
            while (root.children[c] != null) {
                root = root.children[c];
                length++;
                start++;
                if (start == n) {
                    break;
                }
                c = target[start] - 'a';
            }
            return length;
        }

    }

    public int minValidStrings_v1(String[] words, String target) {
        Trie root = new Trie();
        root.build(words);
        char[] chars = target.toCharArray();
        int n = chars.length;
        int[] dp = new int[n];
        Arrays.fill(dp, Integer.MAX_VALUE);
        int length = root.exists(chars, 0);
        for (int i = 0; i < length; i++) {
            dp[i] = 1;
        }

        for (int i = 1; i < n; i++) {
            if (dp[i - 1] == Integer.MAX_VALUE) {
                return -1;
            }
            length = root.exists(chars, i);
            for (int j = i; j < i + length; j++) {
                dp[j] = Math.min(dp[j], dp[i - 1] + 1);
            }
        }

        return dp[n - 1] == Integer.MAX_VALUE ? -1 : dp[n - 1];
    }

}

性能

935.骑士拨号器

目标

象棋骑士有一个独特的移动方式，它可以垂直移动两个方格，水平移动一个方格，或者水平移动两个方格，垂直移动一个方格(两者都形成一个 L 的形状)。

象棋骑士可能的移动方式如下图所示:

我们有一个象棋骑士和一个电话垫，如下所示，骑士只能站在一个数字单元格上(即蓝色单元格)。

给定一个整数 n，返回我们可以拨多少个长度为 n 的不同电话号码。

你可以将骑士放置在任何数字单元格上，然后你应该执行 n - 1 次移动来获得长度为 n 的号码。所有的跳跃应该是有效的骑士跳跃。

因为答案可能很大，所以输出答案模 10^9 + 7.

示例 1：

输入：n = 1
输出：10
解释：我们需要拨一个长度为1的数字，所以把骑士放在10个单元格中的任何一个数字单元格上都能满足条件。

示例 2：

输入：n = 2
输出：20
解释：我们可以拨打的所有有效号码为[04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

示例 3：

输入：n = 3131
输出：136006598
解释：注意取模

说明：

  • 1 <= n <= 5000

思路

有一个电话键盘，布局如下：

1  2  3
4  5  6
7  8  9
*  0  #

开始时，将一个骑士棋子放在数字键上，然后按照国际象棋骑士的走法（类似于中国象棋里的马）走 n - 1 步，问能够组成多少种长度为 n 的不同号码（不能走到 * 和 #）。

这道题与 688.骑士在棋盘上的概率 类似，只不过棋盘更小，状态转移是确定的。

定义 dp[k][i] 表示以 i 结尾长度为 k 的号码组合数。初始时，dp[1][i] 均为 1。状态转移方程，针对不同的数字有所不同，例如 dp[k][1] = dp[k - 1][8] + dp[k - 1][6]，dp[k][4] = dp[k - 1][3] + dp[k - 1][9] + dp[k - 1][0]等等。

1 - 6 - 7
|   |   |
8   0   2
|   |   |
3 - 4 - 9

仔细分析可以得到上面的状态转化图，1 3 7 9 的结果是完全相同的，同理 2 8 也可以认为是一个状态，4 6 是一个状态，0 是一个状态。定义以上 4 个状态为 a b c d，那么最终结果可以表示为 4 * dp[n][a] + 2 * dp[n][b] + 2 * dp[n][c] + dp[n][d]，状态转移方程为：

  • dp[k][a] = dp[k - 1][b] + dp[k - 1][c]
  • dp[k][b] = 2 * dp[k - 1][a]
  • dp[k][c] = 2 * dp[k - 1][a] + dp[k - 1][d]
  • dp[k][d] = 2 * dp[k - 1][c]

注意 k 的初值为 2，k == 1 是特殊情况，骑士可以在数字 5，但是无法继续移动。dp[2][a] = 2, dp[2][b] = 2, dp[2][c] = 3, dp[2][d] = 2

如果写成矩阵的形式 列向量 dp[k] 等于 A · dp[k - 1]，其中矩阵 A 为：

0 1 1 0
2 0 0 0
2 0 0 1
0 0 2 0

因此 dp[n] = A^(n - 1) · dp[1]，其中 dp[1] = [1, 1, 1, 1]。我们可以使用矩阵的快速幂求解。

代码


/**
 * @date 2024-12-10 9:39
 */
public class KnightDialer935 {

    public static int mod = 1000000007;

    public int knightDialer_v3(int n) {
        if (n == 1) {
            return 10;
        }
        long[][] A = new long[][]{
                {0, 1, 1, 0},
                {2, 0, 0, 0},
                {2, 0, 0, 1},
                {0, 0, 2, 0},
        };
        A = pow(A, n - 1);
        long[] res = new long[4];
        for (int i = 0; i < 4; i++) {
            for (int j = 0; j < 4; j++) {
                res[i] += A[i][j];
            }
        }
        return (int) ((4 * res[0] + 2 * res[1] + 2 * res[2] + res[3]) % mod);
    }

    public long[][] pow(long[][] A, int exponent) {
        long[][] res = new long[][]{
                {1, 0, 0, 0},
                {0, 1, 0, 0},
                {0, 0, 1, 0},
                {0, 0, 0, 1},
        };
        while (exponent > 0) {
            if ((exponent & 1) == 1) {
                res = mul(A, res);
            }
            A = mul(A, A);
            exponent >>= 1;
        }
        return res;
    }

    public long[][] mul(long[][] A1, long[][] A2) {
        long[][] res = new long[4][4];
        for (int i = 0; i < 4; i++) {
            for (int k = 0; k < 4; k++) {
                if (A1[i][k] == 0) {
                    continue;
                }
                for (int j = 0; j < 4; j++) {
                    res[i][j] = (res[i][j] + A1[i][k] * A2[k][j]) % mod;
                }
            }
        }
        return res;
    }

    public static long[][] dp;
    public static int MAX = 5001;

    static {
        dp = new long[MAX][4];
        dp[2][0] = 2;
        dp[2][1] = 2;
        dp[2][2] = 3;
        dp[2][3] = 2;
        for (int k = 3; k < MAX; k++) {
            dp[k][0] = (dp[k - 1][1] + dp[k - 1][2]) % mod;
            dp[k][1] = (2 * dp[k - 1][0]) % mod;
            dp[k][2] = (2 * dp[k - 1][0] + dp[k - 1][3]) % mod;
            dp[k][3] = (2 * dp[k - 1][2]) % mod;
        }
    }

    public int knightDialer_v2(int n) {
        if (n == 1) {
            return 10;
        }
        return (int)((4 * dp[n][0] + 2 * dp[n][1] + 2 * dp[n][2] + dp[n][3]) % mod);
    }

    public int knightDialer_v1(int n) {
        long[][] dp = new long[n + 1][10];
        dp[1] = new long[]{1, 1, 1, 1, 1, 1, 1, 1, 1, 1};
        int MOD = 1000000007;
        int res = 0;
        for (int k = 2; k <= n; k++) {
            dp[k][0] = (dp[k - 1][4] + dp[k - 1][6]) % MOD;
            dp[k][1] = (dp[k - 1][6] + dp[k - 1][8]) % MOD;
            dp[k][2] = (dp[k - 1][7] + dp[k - 1][9]) % MOD;
            dp[k][3] = (dp[k - 1][4] + dp[k - 1][8]) % MOD;
            dp[k][4] = (dp[k - 1][3] + dp[k - 1][9] + dp[k - 1][0]) % MOD;
            dp[k][6] = (dp[k - 1][1] + dp[k - 1][7] + dp[k - 1][0]) % MOD;
            dp[k][7] = (dp[k - 1][2] + dp[k - 1][6]) % MOD;
            dp[k][8] = (dp[k - 1][1] + dp[k - 1][3]) % MOD;
            dp[k][9] = (dp[k - 1][2] + dp[k - 1][4]) % MOD;
        }
        for (int i = 0; i < 10; i++) {
            res = (int) (res + dp[n][i]) % MOD;
        }
        return res;
    }

}

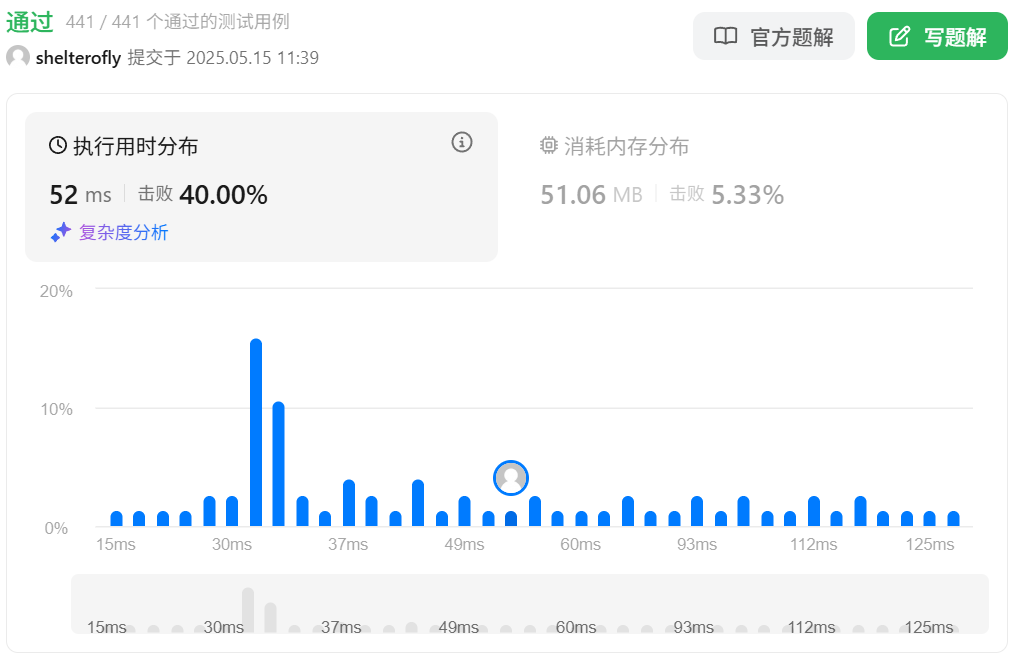
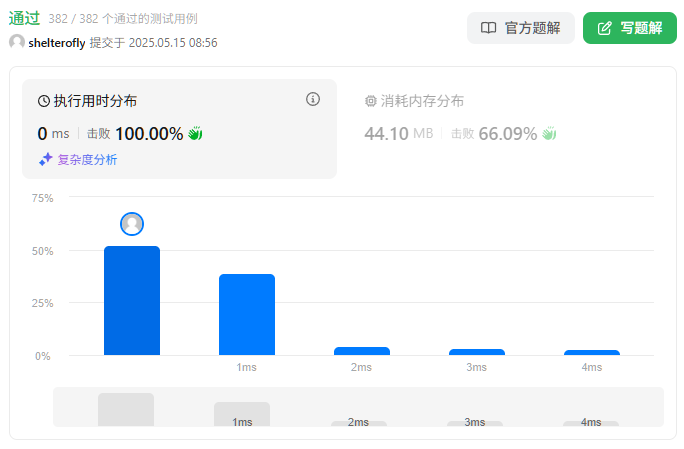
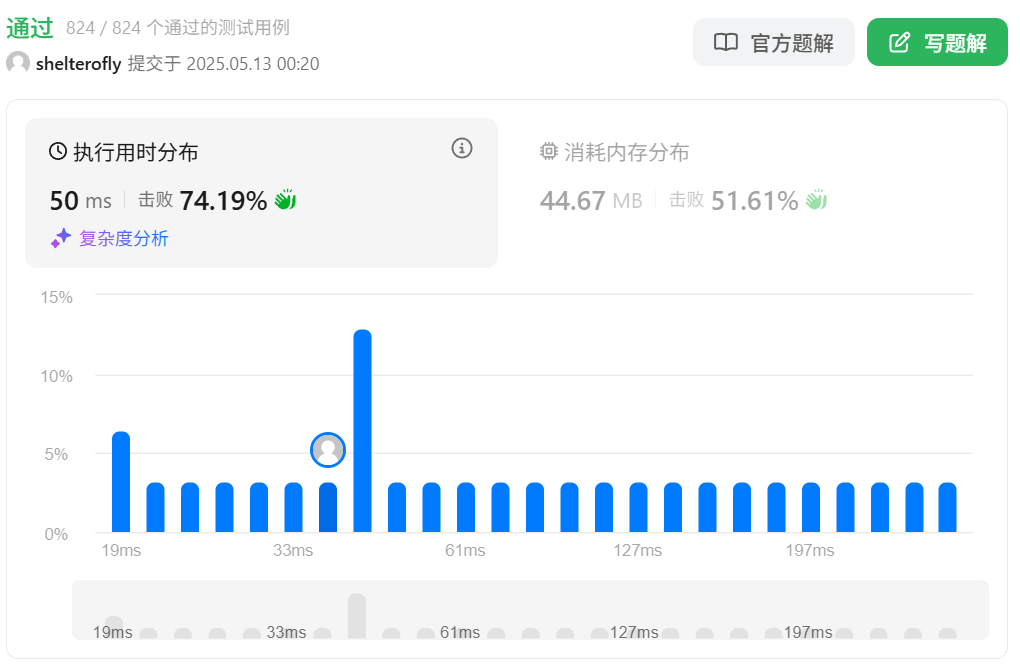
性能