作者： admin

目标

给你一个整数数组 nums 和一个整数 k 。

返回 nums 中一个 非空子数组 的 最大 和，要求该子数组的长度可以 被 k 整除。

示例 1：

输入： nums = [1,2], k = 1
输出： 3
解释：
子数组 [1, 2] 的和为 3，其长度为 2，可以被 1 整除。

示例 2：

输入： nums = [-1,-2,-3,-4,-5], k = 4
输出： -10
解释：
满足题意且和最大的子数组是 [-1, -2, -3, -4]，其长度为 4，可以被 4 整除。

示例 3：

输入： nums = [-5,1,2,-3,4], k = 2
输出： 4
解释：
满足题意且和最大的子数组是 [1, 2, -3, 4]，其长度为 4，可以被 2 整除。

说明：

• 1 <= k <= nums.length <= 2 * 10^5
• -10^9 <= nums[i] <= 10^9

思路

计算长度能被 k 整除的子数组的最大元素和。

核心点是维护同余前缀和的最小值。

也有网友使用滑窗加动态规划来做，滑窗计算 长度为 k 的子数组和，动态规划累加长度 m * k 的子数组和，这里使用了贪心策略，如果前面的子数组和小于 0，直接重置为 0。

代码

/**
 * @date 2025-11-27 9:06
 */
public class MaxSubarraySum3381 {

    public long maxSubarraySum(int[] nums, int k) {
        int n = nums.length;
        long[] prefix = new long[n + 1];
        for (int i = 1; i <= n; i++) {
            prefix[i] = prefix[i - 1] + nums[i - 1];
        }
        long[] minPrefix = new long[k];
        Arrays.fill(minPrefix, Long.MAX_VALUE / 2);
        long res = Long.MIN_VALUE;
        for (int i = 0; i <= n; i++) {
            int rem = i % k;
            res = Math.max(res, prefix[i] - minPrefix[rem]);
            minPrefix[rem] = Math.min(minPrefix[rem], prefix[i]);
        }
        return res;
    }

}

性能

目标

给定正整数 k ，你需要找出可以被 k 整除的、仅包含数字 1 的最 小 正整数 n 的长度。

返回 n 的长度。如果不存在这样的 n ，就返回-1。

注意： n 可能不符合 64 位带符号整数。

示例 1：

输入：k = 1
输出：1
解释：最小的答案是 n = 1，其长度为 1。

示例 2：

输入：k = 2
输出：-1
解释：不存在可被 2 整除的正整数 n 。

示例 3：

输入：k = 3
输出：3
解释：最小的答案是 n = 111，其长度为 3。

说明：

• 1 <= k <= 10^5

思路

求仅包含数字 1 且能够整除正整数 k 的数字的最小长度，如不存在返回 -1。

通俗讲就是多长的 11111…… 能够整除 k。为了防止溢出可以只考虑余数，关键是停止条件是什么？如何确定是否存在？

如果余数出现重复，由于计算的式子不变，后续会陷入循环。可以使用哈希表记录出现过的余数。或者循环 k 次，由于余数的范围只可能是 0 ~ k - 1 共 k 个，如果循环 k 次还没有使余数为 0，那么根据鸽巢原理一定存在重复的余数。

代码

/**
 * @date 2025-11-25 9:26
 */
public class SmallestRepunitDivByK1015 {

    public int smallestRepunitDivByK(int k) {
        if (k == 1) {
            return 1;
        }
        int res = 1;
        int num = 1;
        while (res < k) {
            num = (num * 10 + 1) % k;
            res++;
            if (num == 0) {
                return res;
            }
        }
        return -1;
    }
}

性能

目标

给你一个整数数组 nums，请你找出并返回能被三整除的元素 最大和。

示例 1：

输入：nums = [3,6,5,1,8]
输出：18
解释：选出数字 3, 6, 1 和 8，它们的和是 18（可被 3 整除的最大和）。

示例 2：

输入：nums = [4]
输出：0
解释：4 不能被 3 整除，所以无法选出数字，返回 0。

示例 3：

输入：nums = [1,2,3,4,4]
输出：12
解释：选出数字 1, 3, 4 以及 4，它们的和是 12（可被 3 整除的最大和）。

说明：

• 1 <= nums.length <= 4 * 10^4
• 1 <= nums[i] <= 10^4

思路

求整数数组中元素的最大和，要求和能被 3 整除。

• 如果和 sum % 3 == 1，可以去掉一个模 3 余 1 的最小元素，或者 两个模 3 余 2 的最小元素
• 如果和 sum % 3 == 2，可以去掉一个模 3 余 2 的最小元素，或者 两个模 3 余 1 的最小元素

代码

/**
 * @date 2025-11-23 20:46
 */
public class MaxSumDivThree1262 {

    public int maxSumDivThree(int[] nums) {
        int res = 0;
        PriorityQueue<Integer> q1 = new PriorityQueue<>();
        PriorityQueue<Integer> q2 = new PriorityQueue<>();
        for (int num : nums) {
            res += num;
            if (num % 3 == 1) {
                q1.offer(num);
            } else if (num % 3 == 2) {
                q2.offer(num);
            }
        }
        int mod = res % 3;
        if (mod == 1) {
            int sub = q1.size() == 0 ? 100000 : q1.peek();
            if (q2.size() > 1) {
                sub = Math.min(sub, q2.poll() + q2.poll());
            }
            res -= sub;
        } else if (mod == 2) {
            int sub = q2.size() == 0 ? 100000 : q2.peek();
            if (q1.size() > 1) {
                sub = Math.min(sub, q1.poll() + q1.poll());
            }
            res -= sub;
        }
        return res;
    }
}

性能

目标

给你一个字符串 s ，返回 s 中 长度为 3 的不同回文子序列 的个数。

即便存在多种方法来构建相同的子序列，但相同的子序列只计数一次。

回文 是正着读和反着读一样的字符串。

子序列 是由原字符串删除其中部分字符（也可以不删除）且不改变剩余字符之间相对顺序形成的一个新字符串。

例如，"ace" 是 "abcde" 的一个子序列。

示例 1：

输入：s = "aabca"
输出：3
解释：长度为 3 的 3 个回文子序列分别是：
- "aba" ("aabca" 的子序列)
- "aaa" ("aabca" 的子序列)
- "aca" ("aabca" 的子序列)

示例 2：

输入：s = "adc"
输出：0
解释："adc" 不存在长度为 3 的回文子序列。

示例 3：

输入：s = "bbcbaba"
输出：4
解释：长度为 3 的 4 个回文子序列分别是：
- "bbb" ("bbcbaba" 的子序列)
- "bcb" ("bbcbaba" 的子序列)
- "bab" ("bbcbaba" 的子序列)
- "aba" ("bbcbaba" 的子序列)

说明：

• 3 <= s.length <= 10^5
• s 仅由小写英文字母组成

思路

求长度为 3 的不同回文子序列个数。

枚举中间元素，同时枚举 a - z 作为左右两侧的字母，判断是否前后都存在。

对字母计数，在枚举过程中记录前面出现字母的次数，结合总次数可以快速判断后面是否存在相同的字母。注意，如果前面出现的字母与枚举的中间字母相同需要将次数减 1。

代码

/**
 * @date 2025-11-21 8:44
 */
public class CountPalindromicSubsequence1930 {

    public int countPalindromicSubsequence_v1(String s) {
        int[] total = new int[26];
        char[] chars = s.toCharArray();
        for (char c : chars) {
            total[c - 'a']++;
        }
        boolean[][] visited = new boolean[26][26];
        int[] prefix = new int[26];
        int res = 0;
        for (char c : chars) {
            prefix[c - 'a']++;
            for (int j = 0; j < 26; j++) {
                if (!visited[j][c - 'a'] && total[j] > prefix[j] && ((j == c - 'a' && prefix[j] > 1) || j != c - 'a' && prefix[j] > 0)) {
                    visited[j][c - 'a'] = true;
                    res++;
                }
            }
        }
        return res;
    }

}

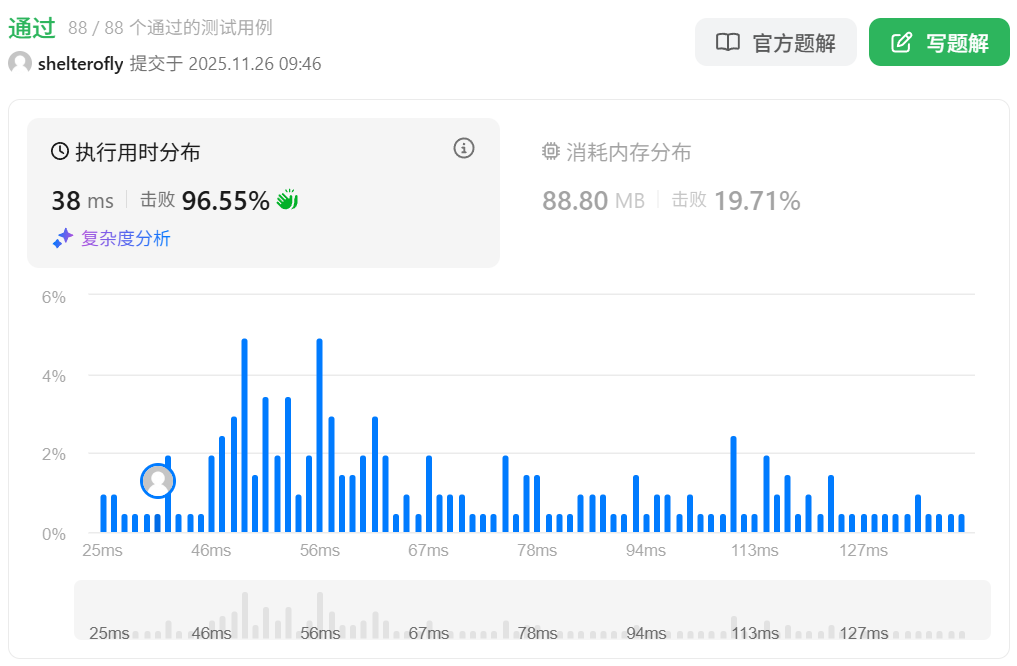
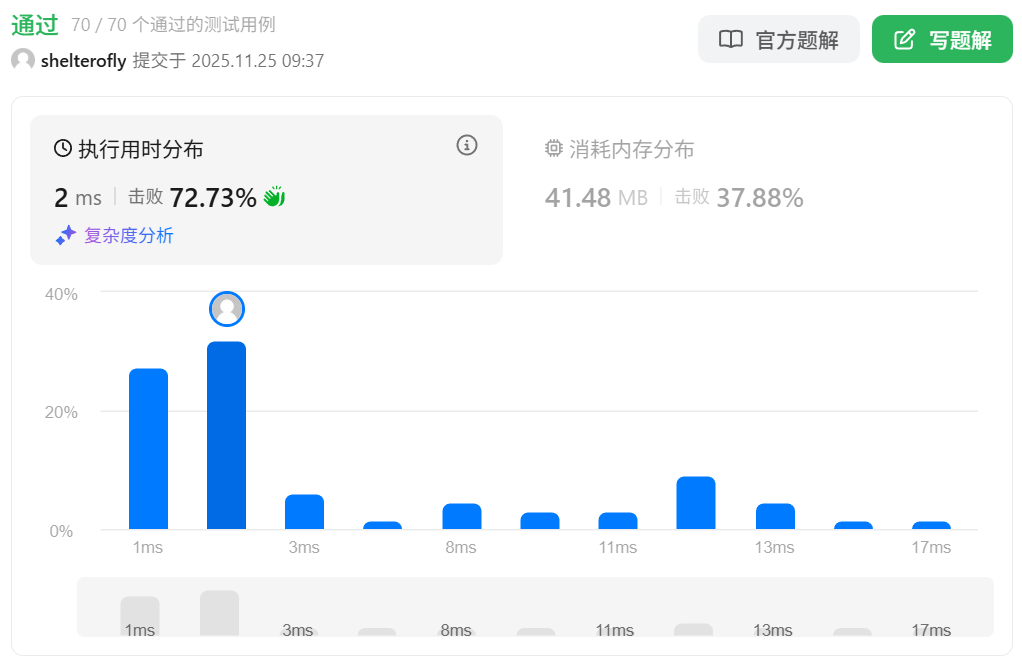
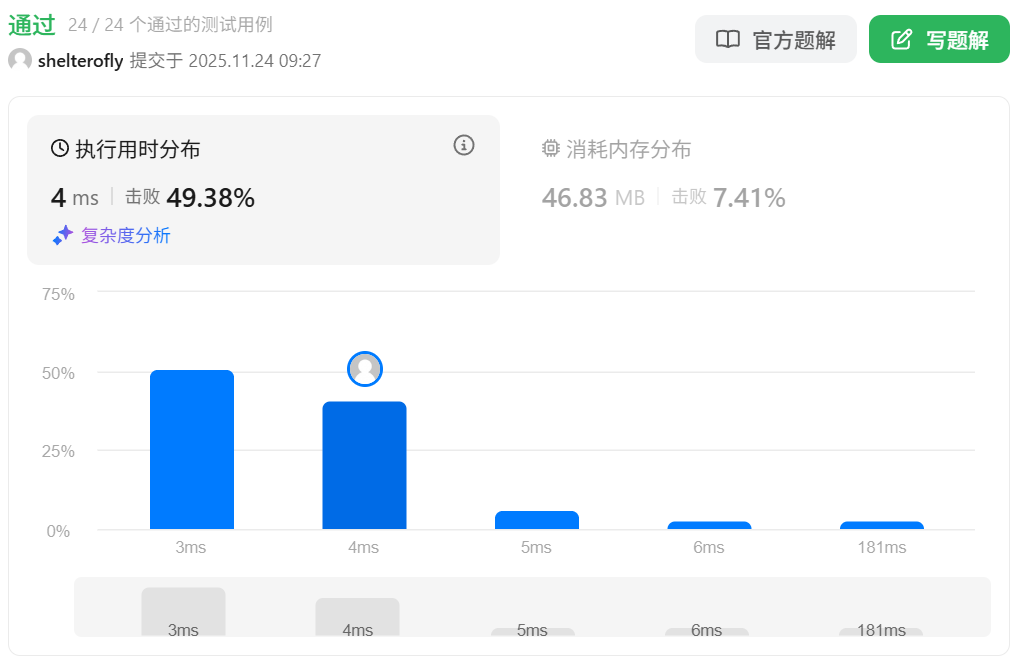
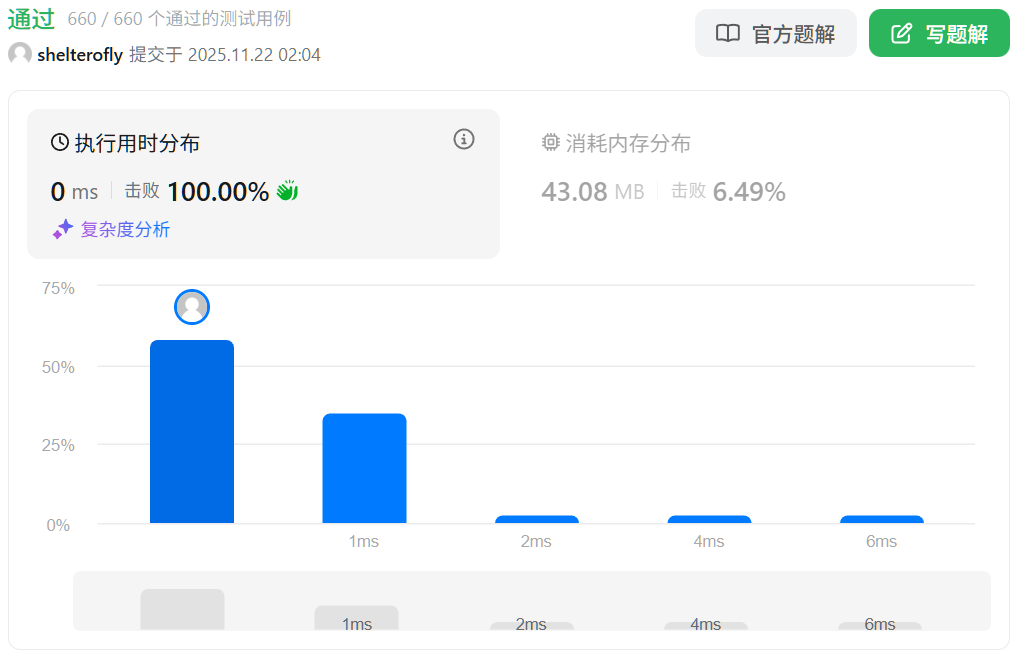
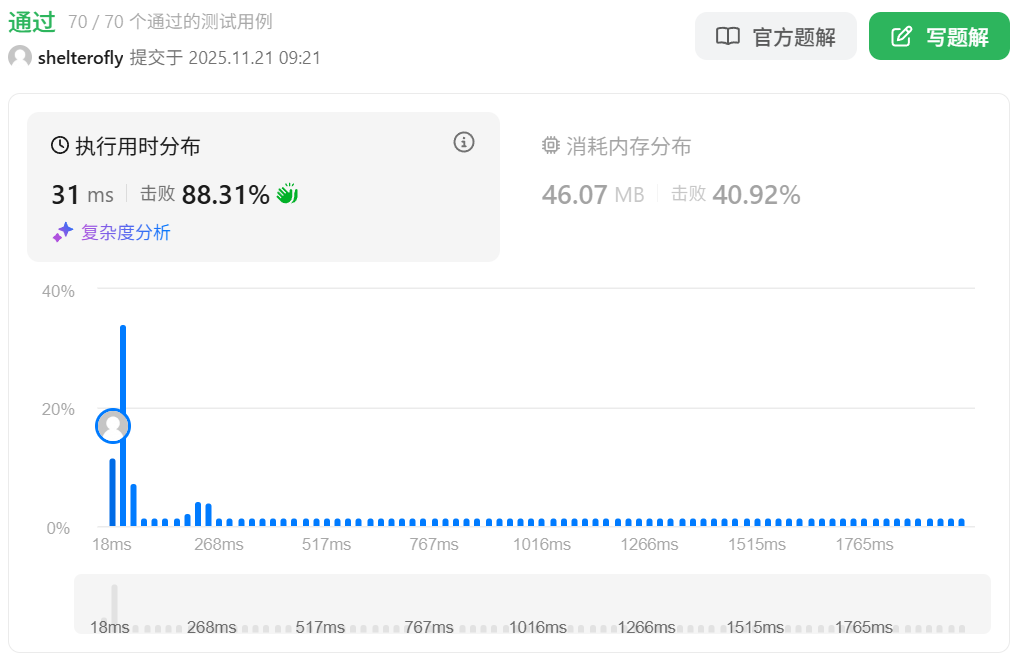
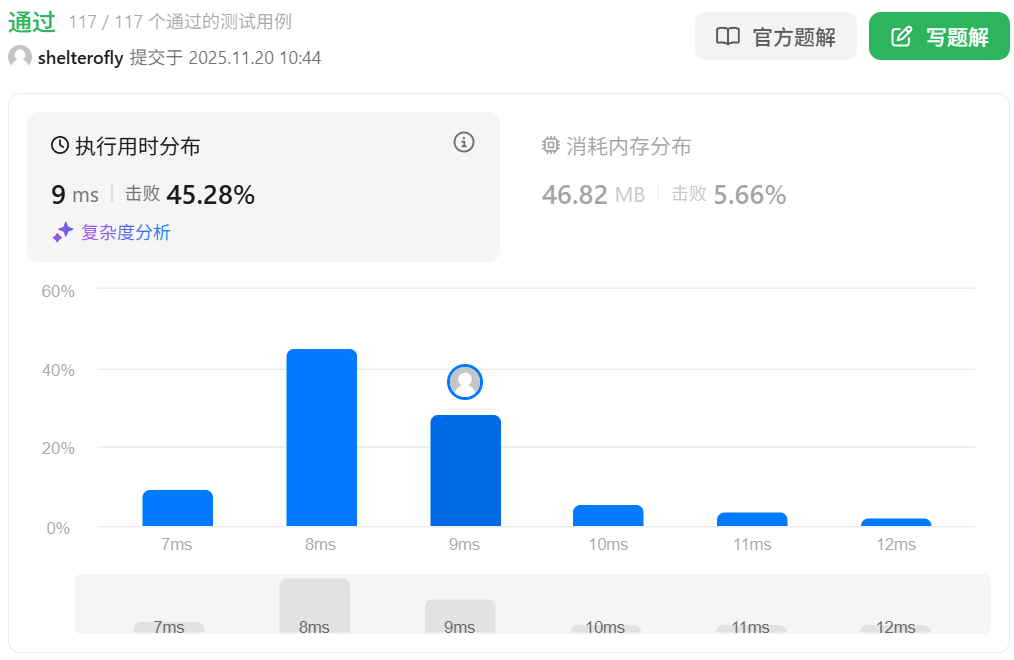
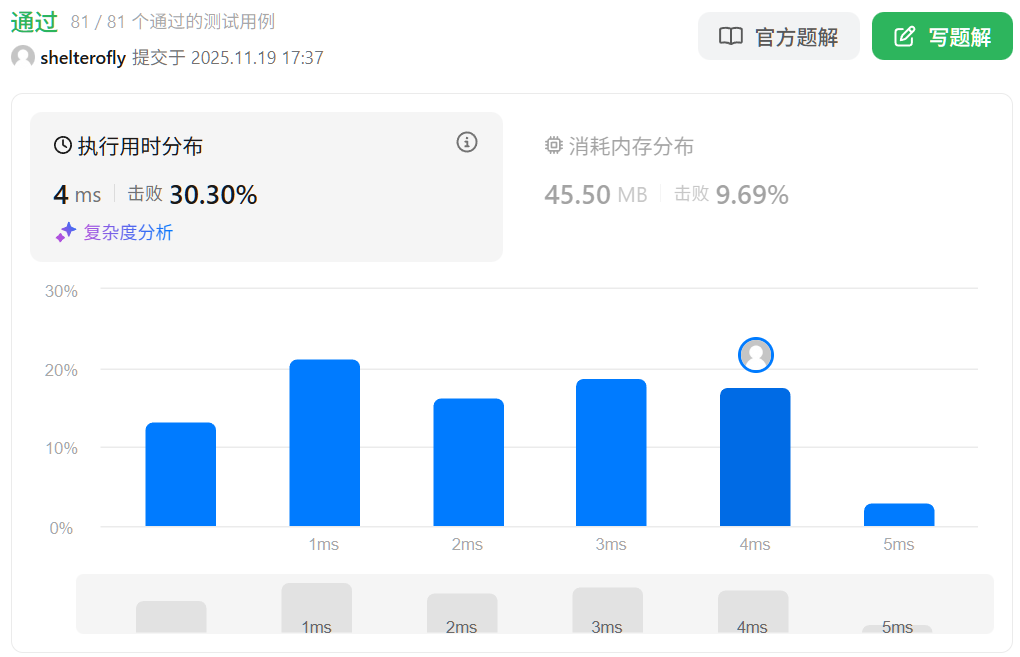
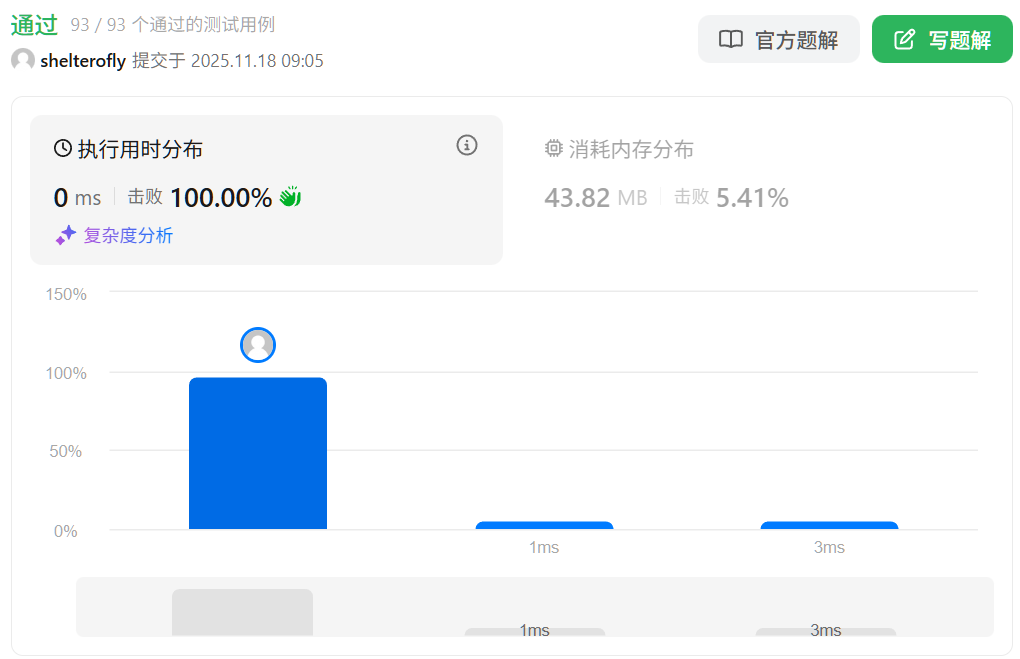
性能