作者： admin

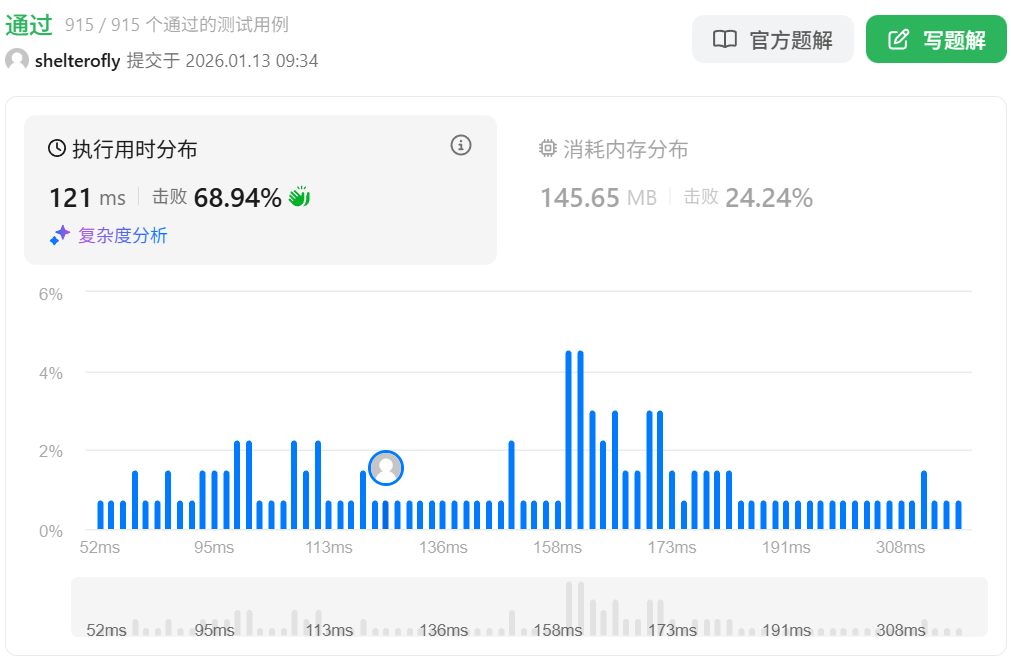
目标

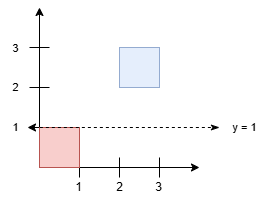
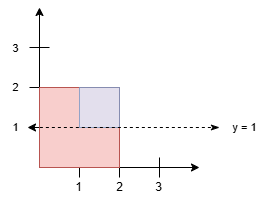
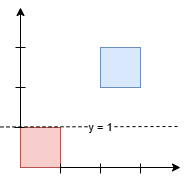
有一个大型的 (m - 1) x (n - 1) 矩形田地，其两个对角分别是 (1, 1) 和 (m, n) ，田地内部有一些水平栅栏和垂直栅栏，分别由数组 hFences 和 vFences 给出。

水平栅栏为坐标 (hFences[i], 1) 到 (hFences[i], n)，垂直栅栏为坐标 (1, vFences[i]) 到 (m, vFences[i]) 。

返回通过 移除 一些栅栏（可能不移除）所能形成的最大面积的 正方形 田地的面积，或者如果无法形成正方形田地则返回 -1。

由于答案可能很大，所以请返回结果对 10^9 + 7 取余 后的值。

注意：田地外围两个水平栅栏（坐标 (1, 1) 到 (1, n) 和坐标 (m, 1) 到 (m, n) ）以及两个垂直栅栏（坐标 (1, 1) 到 (m, 1) 和坐标 (1, n) 到 (m, n) ）所包围。这些栅栏 不能 被移除。

示例 1：

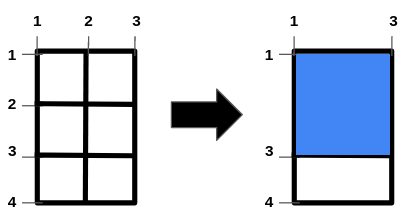
输入：m = 4, n = 3, hFences = [2,3], vFences = [2]
输出：4
解释：移除位于 2 的水平栅栏和位于 2 的垂直栅栏将得到一个面积为 4 的正方形田地。

示例 2：

输入：m = 6, n = 7, hFences = [2], vFences = [4]
输出：-1
解释：可以证明无法通过移除栅栏形成正方形田地。

说明：

• 3 <= m, n <= 10^9
• 1 <= hFences.length, vFences.length <= 600
• 1 < hFences[i] < m
• 1 < vFences[i] < n
• hFences 和 vFences 中的元素是唯一的。

思路

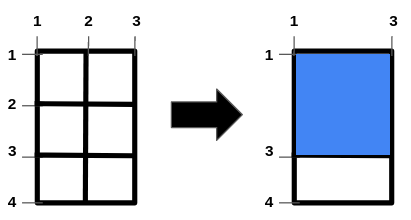
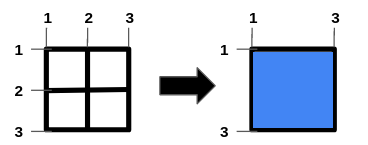
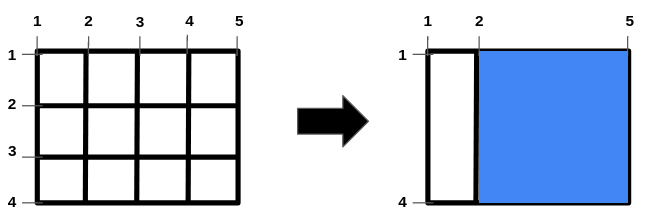
有一个 (m - 1) x (n - 1) 矩形田地，左上角坐标为 (1, 1)，右下角坐标为 (m, n)，田地内部有一些栅栏，水平栅栏 i 的纵坐标为 hFences[i]，垂直栅栏 j 的横坐标为 vFences[j]。可以移除一些栅栏，求能够形成的最大正方形的面积。

使用哈希表分别记录水平与垂直方向可能的间隔，找到最大相等间隔，相乘即可。

代码

/**
 * @date 2026-01-16 8:49
 */
public class MaximizeSquareArea2975 {

    public int maximizeSquareArea(int m, int n, int[] hFences, int[] vFences) {
        Set<Integer> hq = getInterval(m, hFences);
        Set<Integer> vq = getInterval(n, vFences);
        hq.retainAll(vq);
        if (hq.size() == 0) {
            return -1;
        }
        long res = 0;
        int mod = 1000000007;
        for (Integer num : hq) {
            res = Math.max(res, num);
        }
        return (int) (res * res % mod);
    }

    private Set<Integer> getInterval(int edge, int[] fences) {
        Arrays.sort(fences);
        Set<Integer> set = new HashSet<>();
        int n = fences.length;
        for (int i = 0; i < n; i++) {
            set.add(fences[i] - 1);
            set.add(edge - fences[i]);
            for (int j = i + 1; j < n; j++) {
                set.add(fences[j] - fences[i]);
            }
        }
        set.add(edge - 1);
        return set;
    }

}

性能

目标

给你一个网格图，由 n + 2 条 横线段 和 m + 2 条 竖线段 组成，一开始所有区域均为 1 x 1 的单元格。

所有线段的编号从 1 开始。

给你两个整数 n 和 m 。

同时给你两个整数数组 hBars 和 vBars 。

• hBars 包含区间 [2, n + 1] 内 互不相同 的横线段编号。
• vBars 包含 [2, m + 1] 内 互不相同的 竖线段编号。

如果满足以下条件之一，你可以 移除 两个数组中的部分线段：

• 如果移除的是横线段，它必须是 hBars 中的值。
• 如果移除的是竖线段，它必须是 vBars 中的值。

请你返回移除一些线段后（可能不移除任何线段），剩余网格图中 最大正方形 空洞的面积，正方形空洞的意思是正方形 内部 不含有任何线段。

示例 1：

输入：n = 2, m = 1, hBars = [2,3], vBars = [2]
输出：4
解释：左边的图是一开始的网格图。
横线编号的范围是区间 [1,4] ，竖线编号的范围是区间 [1,3] 。
可以移除的横线段为 [2,3] ，竖线段为 [2] 。
一种得到最大正方形面积的方法是移除横线段 2 和竖线段 2 。
操作后得到的网格图如右图所示。
正方形空洞面积为 4。
无法得到面积大于 4 的正方形空洞。
所以答案为 4 。

示例 2：

输入：n = 1, m = 1, hBars = [2], vBars = [2]
输出：4
解释：左边的图是一开始的网格图。
横线编号的范围是区间 [1,3] ，竖线编号的范围是区间 [1,3] 。
可以移除的横线段为 [2] ，竖线段为 [2] 。
一种得到最大正方形面积的方法是移除横线段 2 和竖线段 2 。
操作后得到的网格图如右图所示。
正方形空洞面积为 4。
无法得到面积大于 4 的正方形空洞。
所以答案为 4 。

示例 3：

输入：n = 2, m = 3, hBars = [2,3], vBars = [2,3,4]
输出：9
解释：左边的图是一开始的网格图。
横线编号的范围是区间 [1,4] ，竖线编号的范围是区间 [1,5] 。
可以移除的横线段为 [2,3] ，竖线段为 [2,3,4] 。
一种得到最大正方形面积的方法是移除横线段 2、3 和竖线段 3、4 。
操作后得到的网格图如右图所示。
正方形空洞面积为 9。
无法得到面积大于 9 的正方形空洞。
所以答案为 9 。

说明：

• 1 <= n <= 10^9
• 1 <= m <= 10^9
• 1 <= hBars.length <= 100
• 2 <= hBars[i] <= n + 1
• 1 <= vBars.length <= 100
• 2 <= vBars[i] <= m + 1
• hBars 中的值互不相同。
• vBars 中的值互不相同。

思路

有一个网格图由 n + 2 条横线段编号为 1 ~ n + 2 和 m + 2 条竖线段编号为 1 ~ m + 2 组成，单元格为 1 x 1，即横线间隔为 1，竖线间隔为 1。有两个数组 hBars 与 vBars，给出了横线段的编号 2 ~ n + 1 与竖线段编号 2 ~ m + 1 内的线段。删除其中的一些线段，使得空洞的正方形面积最大，返回面积的最大值。

要使空洞最大，能删尽删，找出两个数组线段编号连续的长度最大值，取二者的最小值（正方形），加一（删掉 k 条线段，空洞的边长为 k + 1）后平方即可。

代码

/**
 * @date 2026-01-15 9:08
 */
public class MaximizeSquareHoleArea2943 {

    public int maximizeSquareHoleArea(int n, int m, int[] hBars, int[] vBars) {
        Arrays.sort(hBars);
        Arrays.sort(vBars);
        int hmax = getMaxInterval(hBars);
        int vmax = getMaxInterval(vBars);
        int min = Math.min(hmax, vmax) + 1;
        return min * min;
    }

    private int getMaxInterval_v1(int[] bars) {
        int l = bars.length;
        int max = 1;
        int i = 0;
        while (i < l - 1) {
            int start = i;
            do {
                i++;
            } while (i < l && bars[i - 1] + 1 == bars[i]);
            max = Math.max(max, i - start);
        }
        return max;
    }

}

性能

目标

给你一个二维整数数组 squares ，其中 squares[i] = [xi, yi, li] 表示一个与 x 轴平行的正方形的左下角坐标和正方形的边长。

找到一个最小的 y 坐标，它对应一条水平线，该线需要满足它以上正方形的总面积 等于 该线以下正方形的总面积。

答案如果与实际答案的误差在 10^-5 以内，将视为正确答案。

注意：正方形 可能会 重叠。重叠区域应该被 多次计数 。

示例 1：

输入： squares = [[0,0,1],[2,2,1]]
输出： 1.00000
解释：
任何在 y = 1 和 y = 2 之间的水平线都会有 1 平方单位的面积在其上方，1 平方单位的面积在其下方。最小的 y 坐标是 1。

示例 2：

输入： squares = [[0,0,2],[1,1,1]]
输出： 1.16667
解释：
面积如下：
线下的面积：7/6 * 2 (红色) + 1/6 (蓝色) = 15/6 = 2.5。
线上的面积：5/6 * 2 (红色) + 5/6 (蓝色) = 15/6 = 2.5。
由于线以上和线以下的面积相等，输出为 7/6 = 1.16667。

说明：

• 1 <= squares.length <= 5 * 10^4
• squares[i] = [xi, yi, li]
• squares[i].length == 3
• 0 <= xi, yi <= 10^9
• 1 <= li <= 10^9
• 所有正方形的总面积不超过 10^12。

思路

二维平面内有一些正方形，squares[i] = [xi, yi, li] 表示正方形坐下顶点坐标为 (xi, yi)，边长为 li。找到最小的 y 水平线，使得这些正方形在水平线上方的面积等于下方的面积，重叠部分的面积应被重复计算。

二分答案，计算上方与下方的面积。

代码

/**
 * @date 2026-01-13 9:08
 */
public class SeparateSquares3453 {

    public double separateSquares(int[][] squares) {
        double l = 0.0, r = 1000000000.0;
        double m = l + (r - l) / 2;
        while (l <= r) {
            if (check(squares, m)) {
                r = m - 0.00001;
            } else {
                l = m + 0.00001;
            }
            m = l + (r - l) / 2;
        }
        return l;
    }

    private boolean check(int[][] squares, double m) {
        double upperSum = 0.0, lowerSum = 0.0;
        for (int[] square : squares) {
            int y = square[1], l = square[2];
            if (y + l <= m) {
                lowerSum += (double) l * l;
            } else if (y >= m) {
                upperSum += (double) l * l;
            } else {
                upperSum += (double) l * (y + l - m);
                lowerSum += (double) l * (m - y);
            }
        }
        return upperSum <= lowerSum;
    }

}

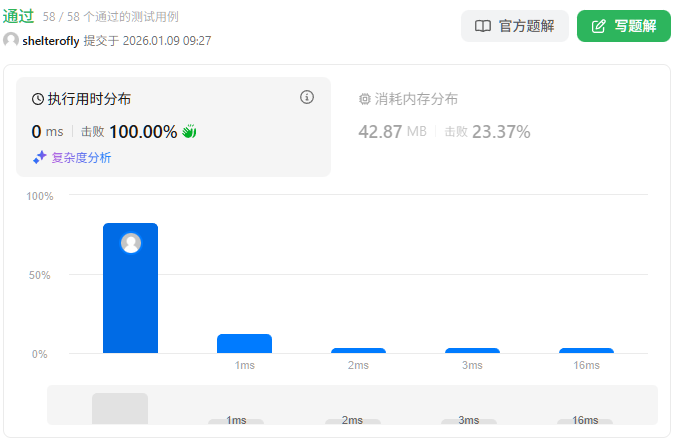
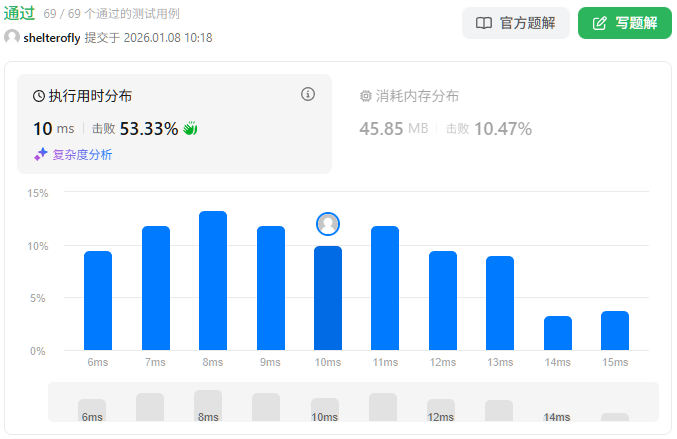
性能