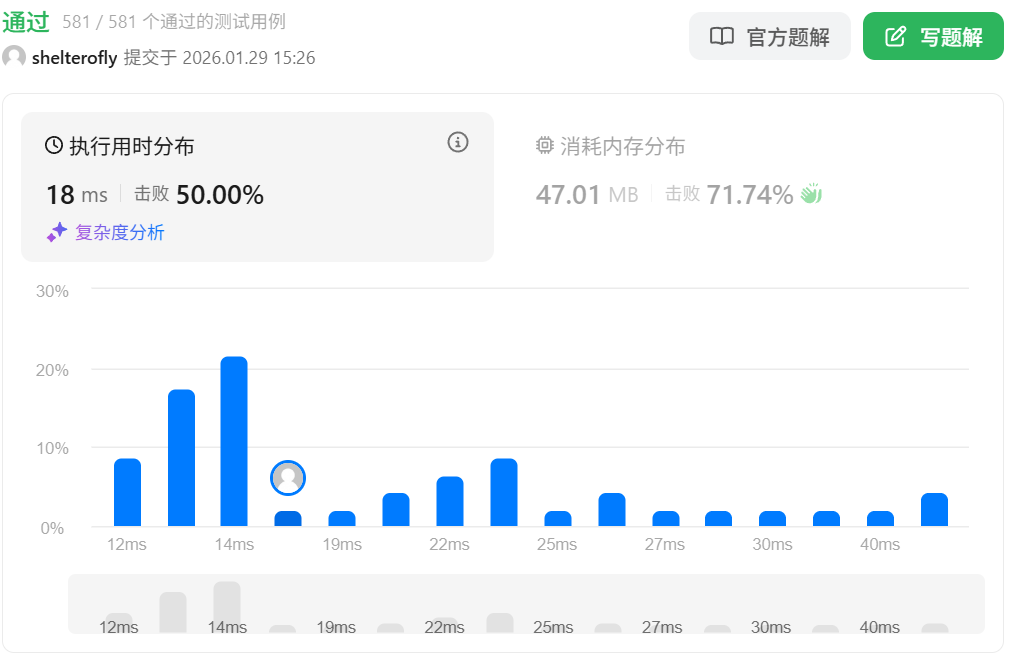
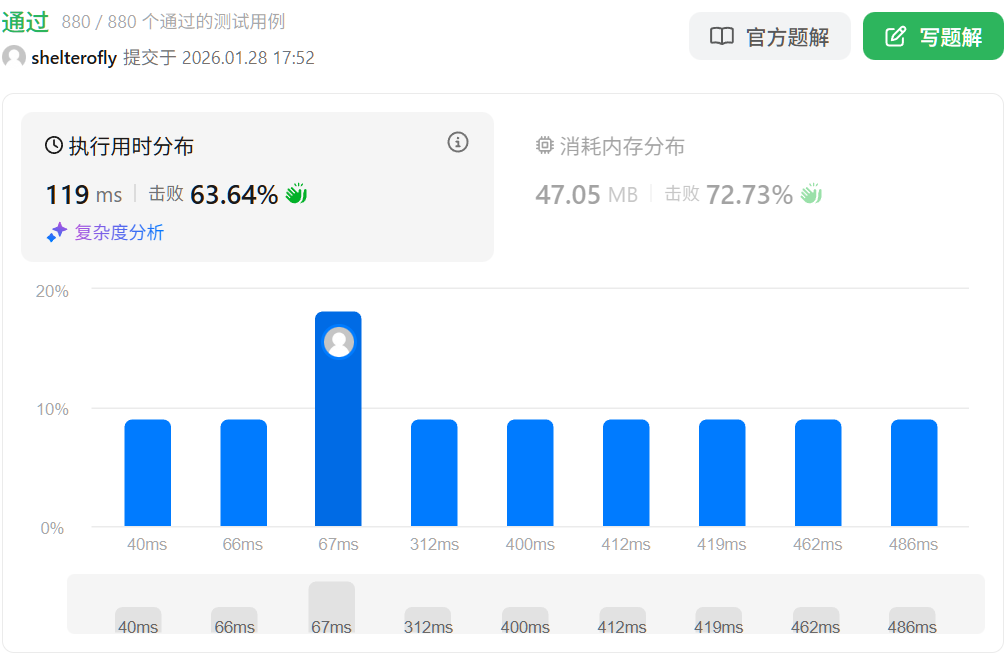
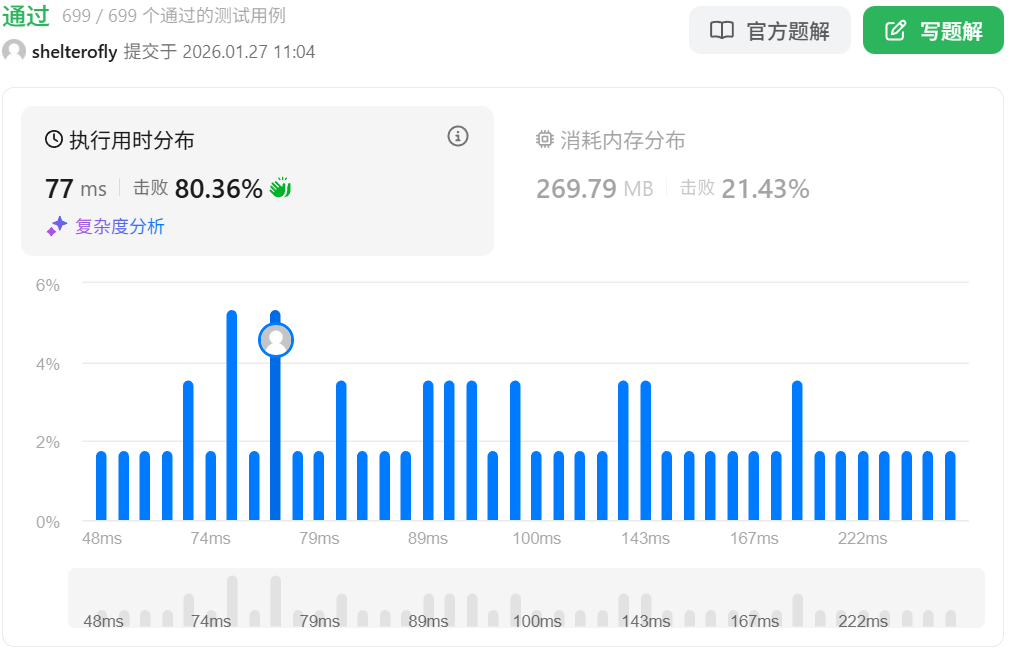
目标
给你两个下标从 0 开始的字符串 source 和 target ,它们的长度均为 n 并且由 小写 英文字母组成。
另给你两个下标从 0 开始的字符串数组 original 和 changed ,以及一个整数数组 cost ,其中 cost[i] 代表将字符串 original[i] 更改为字符串 changed[i] 的成本。
你从字符串 source 开始。在一次操作中,如果 存在 任意 下标 j 满足 cost[j] == z 、original[j] == x 以及 changed[j] == y ,你就可以选择字符串中的 子串 x 并以 z 的成本将其更改为 y 。 你可以执行 任意数量 的操作,但是任两次操作必须满足 以下两个 条件 之一 :
- 在两次操作中选择的子串分别是 source[a..b] 和 source[c..d] ,满足 b < c 或 d < a 。换句话说,两次操作中选择的下标 不相交 。
- 在两次操作中选择的子串分别是 source[a..b] 和 source[c..d] ,满足 a == c 且 b == d 。换句话说,两次操作中选择的下标 相同 。
返回将字符串 source 转换为字符串 target 所需的 最小 成本。如果不可能完成转换,则返回 -1 。
注意,可能存在下标 i 、j 使得 original[j] == original[i] 且 changed[j] == changed[i] 。
示例 1:
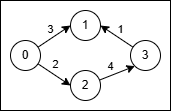
输入:source = "abcd", target = "acbe", original = ["a","b","c","c","e","d"], changed = ["b","c","b","e","b","e"], cost = [2,5,5,1,2,20]
输出:28
解释:将 "abcd" 转换为 "acbe",执行以下操作:
- 将子串 source[1..1] 从 "b" 改为 "c" ,成本为 5 。
- 将子串 source[2..2] 从 "c" 改为 "e" ,成本为 1 。
- 将子串 source[2..2] 从 "e" 改为 "b" ,成本为 2 。
- 将子串 source[3..3] 从 "d" 改为 "e" ,成本为 20 。
产生的总成本是 5 + 1 + 2 + 20 = 28 。
可以证明这是可能的最小成本。示例 2:
输入:source = "abcdefgh", target = "acdeeghh", original = ["bcd","fgh","thh"], changed = ["cde","thh","ghh"], cost = [1,3,5]
输出:9
解释:将 "abcdefgh" 转换为 "acdeeghh",执行以下操作:
- 将子串 source[1..3] 从 "bcd" 改为 "cde" ,成本为 1 。
- 将子串 source[5..7] 从 "fgh" 改为 "thh" ,成本为 3 。可以执行此操作,因为下标 [5,7] 与第一次操作选中的下标不相交。
- 将子串 source[5..7] 从 "thh" 改为 "ghh" ,成本为 5 。可以执行此操作,因为下标 [5,7] 与第一次操作选中的下标不相交,且与第二次操作选中的下标相同。
产生的总成本是 1 + 3 + 5 = 9 。
可以证明这是可能的最小成本。示例 3:
输入:source = "abcdefgh", target = "addddddd", original = ["bcd","defgh"], changed = ["ddd","ddddd"], cost = [100,1578]
输出:-1
解释:无法将 "abcdefgh" 转换为 "addddddd" 。
如果选择子串 source[1..3] 执行第一次操作,以将 "abcdefgh" 改为 "adddefgh" ,你无法选择子串 source[3..7] 执行第二次操作,因为两次操作有一个共用下标 3 。
如果选择子串 source[3..7] 执行第一次操作,以将 "abcdefgh" 改为 "abcddddd" ,你无法选择子串 source[1..3] 执行第二次操作,因为两次操作有一个共用下标 3 。说明:
- 1 <= source.length == target.length <= 1000
- source、target 均由小写英文字母组成
- 1 <= cost.length == original.length == changed.length <= 100
- 1 <= original[i].length == changed[i].length <= source.length
- original[i]、changed[i] 均由小写英文字母组成
- original[i] != changed[i]
- 1 <= cost[i] <= 10^6
思路
代码