目标
给你一个包含 n 个节点的有向带权图,节点编号从 0 到 n - 1。同时给你一个数组 edges,其中 edges[i] = [ui, vi, wi] 表示一条从节点 ui 到节点 vi 的有向边,其成本为 wi。
每个节点 ui 都有一个 最多可使用一次 的开关:当你到达 ui 且尚未使用其开关时,你可以对其一条入边 vi → ui 激活开关,将该边反转为 ui → vi 并 立即 穿过它。
反转仅对那一次移动有效,使用反转边的成本为 2 * wi。
返回从节点 0 到达节点 n - 1 的 最小 总成本。如果无法到达,则返回 -1。
示例 1:
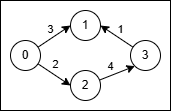
输入: n = 4, edges = [[0,1,3],[3,1,1],[2,3,4],[0,2,2]]
输出: 5
解释:
使用路径 0 → 1 (成本 3)。
在节点 1,将原始边 3 → 1 反转为 1 → 3 并穿过它,成本为 2 * 1 = 2。
总成本为 3 + 2 = 5。示例 2:
输入: n = 4, edges = [[0,2,1],[2,1,1],[1,3,1],[2,3,3]]
输出: 3
解释:
不需要反转。走路径 0 → 2 (成本 1),然后 2 → 1 (成本 1),再然后 1 → 3 (成本 1)。
总成本为 1 + 1 + 1 = 3。说明:
- 2 <= n <= 5 * 10^4
- 1 <= edges.length <= 10^5
- edges[i] = [ui, vi, wi]
- 0 <= ui, vi <= n - 1
- 1 <= wi <= 1000
思路
有一个包含 n 个节点的有向带权图,节点编号为 0 ~ n - 1,对于每一条有向边可以将其方向反转一次,代价是权重的 2 倍,求 从 0 到 n - 1 的最小路径成本。
建图,将一个方向的边同时建立双向连接,反向的权重乘以 2。然后使用 dijkstra 算法求最短路径即可。
代码
/**
* @date 2026-01-27 8:54
*/
public class MinCost3650 {
public int minCost(int n, int[][] edges) {
List<int[]>[] g = new ArrayList[n];
Arrays.setAll(g, l -> new ArrayList<>());
for (int[] edge : edges) {
int u = edge[0];
int v = edge[1];
int w = edge[2];
g[u].add(new int[]{v, w});
g[v].add(new int[]{u, 2 * w});
}
return dijkstra(g, 0, n - 1);
}
public int dijkstra(List<int[]>[] g, int start, int end) {
int n = g.length;
int[] dist = new int[n];
Arrays.fill(dist, Integer.MAX_VALUE);
dist[start] = 0;
PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> a[1] - b[1]);
q.offer(new int[]{start, 0});
while (!q.isEmpty()) {
int[] from = q.poll();
int cur = from[0];
int cost = from[1];
if (cost > dist[cur]) {
continue;
}
if (cur == end) {
return cost;
}
for (int[] edge : g[cur]) {
int next = edge[0];
int weight = edge[1];
if (dist[cur] + weight < dist[next]) {
dist[next] = dist[cur] + weight;
q.offer(new int[]{next, dist[next]});
}
}
}
return -1;
}
}
性能