目标
给你一个整数 eventTime 表示一个活动的总时长,这个活动开始于 t = 0 ,结束于 t = eventTime 。
同时给你两个长度为 n 的整数数组 startTime 和 endTime 。它们表示这次活动中 n 个时间 没有重叠 的会议,其中第 i 个会议的时间为 [startTime[i], endTime[i]] 。
你可以重新安排 至多 k 个会议,安排的规则是将会议时间平移,且保持原来的 会议时长 ,你的目的是移动会议后 最大化 相邻两个会议之间的 最长 连续空余时间。
移动前后所有会议之间的 相对 顺序需要保持不变,而且会议时间也需要保持互不重叠。
请你返回重新安排会议以后,可以得到的 最大 空余时间。
注意,会议 不能 安排到整个活动的时间以外。
示例 1:
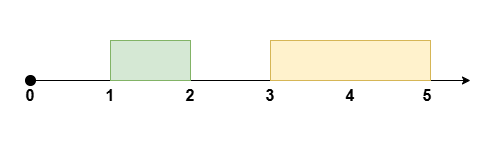
输入:eventTime = 5, k = 1, startTime = [1,3], endTime = [2,5]
输出:2
解释:
将 [1, 2] 的会议安排到 [2, 3] ,得到空余时间 [0, 2] 。示例 2:
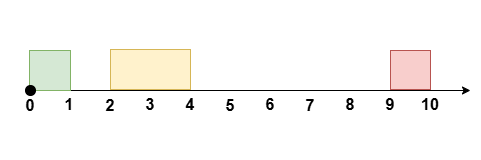
输入:eventTime = 10, k = 1, startTime = [0,2,9], endTime = [1,4,10]
输出:6
解释:
将 [2, 4] 的会议安排到 [1, 3] ,得到空余时间 [3, 9] 。示例 3:
输入:eventTime = 5, k = 2, startTime = [0,1,2,3,4], endTime = [1,2,3,4,5]
输出:0
解释:
活动中的所有时间都被会议安排满了。说明:
- 1 <= eventTime <= 10^9
- n == startTime.length == endTime.length
- 2 <= n <= 10^5
- 1 <= k <= n
- 0 <= startTime[i] < endTime[i] <= eventTime
- endTime[i] <= startTime[i + 1] 其中 i 在范围 [0, n - 2] 之间。
思路
有一个活动有 n 个时间不重叠的会议,重新安排 k 个会议议程,使得空余时间最大。
先根据会议时间排序,滑动窗口计算 k 个会议的总时间,以及 [end[l - 1], start[r + 1]],相减即为窗口内的最大空余时间。
代码
/**
* @date 2025-07-09 8:52
*/
public class MaxFreeTime3439 {
public int maxFreeTime(int eventTime, int k, int[] startTime, int[] endTime) {
int n = startTime.length;
int[][] interval = new int[n + 2][2];
interval[0][1] = 0;
for (int i = 1; i <= n; i++) {
interval[i] = new int[]{startTime[i - 1], endTime[i - 1]};
}
interval[n + 1][0] = eventTime;
int l = 1;
int res = 0, sum = 0;
for (int r = 1; r <= n; r++) {
sum += interval[r][1] - interval[r][0];
if (r - l == k - 1) {
res = Math.max(res, interval[r + 1][0] - interval[l - 1][1] - sum);
sum -= interval[l][1] - interval[l][0];
l++;
}
}
return res;
}
}
性能