目标
一个 k x k 的 幻方 指的是一个 k x k 填满整数的方格阵,且每一行、每一列以及两条对角线的和 全部相等 。幻方中的整数 不需要互不相同 。显然,每个 1 x 1 的方格都是一个幻方。
给你一个 m x n 的整数矩阵 grid ,请你返回矩阵中 最大幻方 的 尺寸 (即边长 k)。
示例 1:
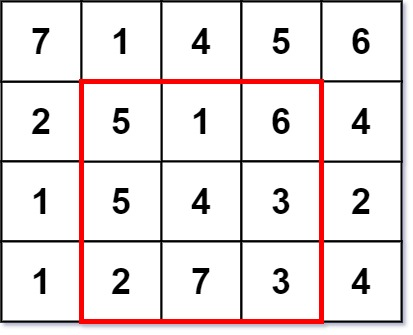
输入:grid = [[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]]
输出:3
解释:最大幻方尺寸为 3 。
每一行,每一列以及两条对角线的和都等于 12 。
- 每一行的和:5+1+6 = 5+4+3 = 2+7+3 = 12
- 每一列的和:5+5+2 = 1+4+7 = 6+3+3 = 12
- 对角线的和:5+4+3 = 6+4+2 = 12示例 2:
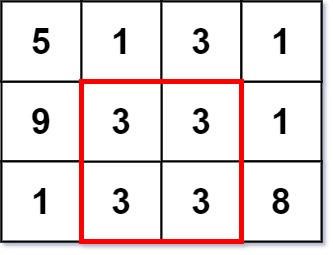
输入:grid = [[5,1,3,1],[9,3,3,1],[1,3,3,8]]
输出:2说明:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 50
- 1 <= grid[i][j] <= 10^6
思路
找出 m x n 矩阵中的最大幻方的边长。
暴力枚举顶点与边长,判断是否是幻方。可以记录水平、垂直、主对角线和副对角线上的前缀和,方便幻方判断。另外边长可以从大到小枚举,是幻方就直接返回。
代码
/**
* @date 2026-01-19 14:59
*/
public class LargestMagicSquare1895 {
public int largestMagicSquare(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int res = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
int l = Math.min(i, j) + 1;
for (int k = res + 1; k <= l; k++) {
if (isMagicSquare(grid, i, j, k)) {
res = k;
}
}
}
}
return res;
}
public boolean isMagicSquare(int[][] grid, int x, int y, int l) {
int diagonal1 = 0;
int diagonal2 = 0;
for (int k = 0; k < l; k++) {
diagonal1 += grid[x - k][y - k];
diagonal2 += grid[x - l + 1 + k][y - k];
}
if (diagonal1 != diagonal2) {
return false;
}
for (int i = x - l + 1; i <= x; i++) {
int sum = 0;
for (int j = y - l + 1; j <= y; j++) {
sum += grid[i][j];
}
if (sum != diagonal1) {
return false;
}
}
for (int j = y - l + 1; j <= y; j++) {
int sum = 0;
for (int i = x - l + 1; i <= x; i++) {
sum += grid[i][j];
}
if (sum != diagonal1) {
return false;
}
}
return true;
}
}
性能