目标
数字小镇 Digitville 中,存在一个数字列表 nums,其中包含从 0 到 n - 1 的整数。每个数字本应 只出现一次,然而,有 两个 顽皮的数字额外多出现了一次,使得列表变得比正常情况下更长。
为了恢复 Digitville 的和平,作为小镇中的名侦探,请你找出这两个顽皮的数字。
返回一个长度为 2 的数组,包含这两个数字(顺序任意)。
示例 1:
输入: nums = [0,1,1,0]
输出: [0,1]
解释:
数字 0 和 1 分别在数组中出现了两次。示例 2:
输入: nums = [0,3,2,1,3,2]
输出: [2,3]
解释:
数字 2 和 3 分别在数组中出现了两次。示例 3:
输入: nums = [7,1,5,4,3,4,6,0,9,5,8,2]
输出: [4,5]
解释:
数字 4 和 5 分别在数组中出现了两次。说明:
- 2 <= n <= 100
- nums.length == n + 2
- 0 <= nums[i] < n
- 输入保证 nums 中 恰好 包含两个重复的元素。
思路
长度为 n + 2 的数组,其元素由 0 1 2 …… n - 1 n 个数字以及该范围内的两个任意数字组成,找出这两个重复数字。
简单的做法是对每个元素计数,找出出现次数为 2 的元素。但是空间复杂度为 O(n)。
进阶的做法是使用位运算得到这两个重复数字的异或值,这两个数字至少有一个 bit 位不同,根据该 bit 位分组,最终得到这两个数字。
代码
/**
* @date 2025-10-31 9:05
*/
public class GetSneakyNumbers3289 {
public int[] getSneakyNumbers(int[] nums) {
int n = nums.length;
int[] cnt = new int[n];
List<Integer> list = new ArrayList<>();
for (int num : nums) {
cnt[num]++;
if (cnt[num] == 2){
list.add(num);
}
}
int[] res = new int[2];
for (int i = 0; i < 2; i++) {
res[i] = list.get(i);
}
return res;
}
}
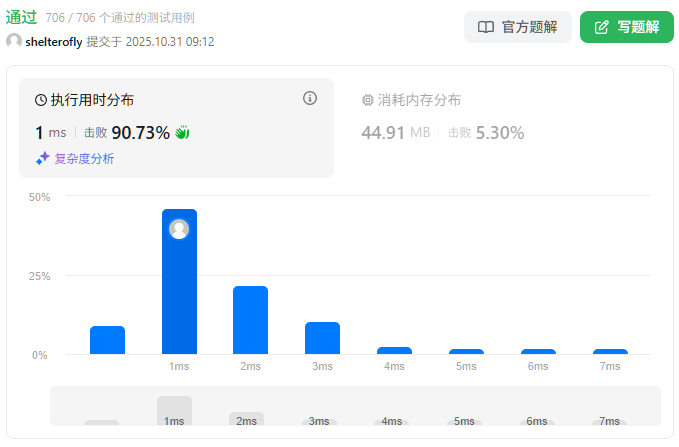
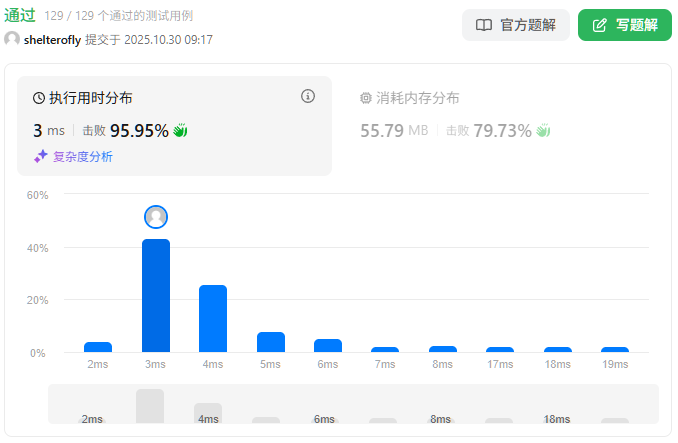
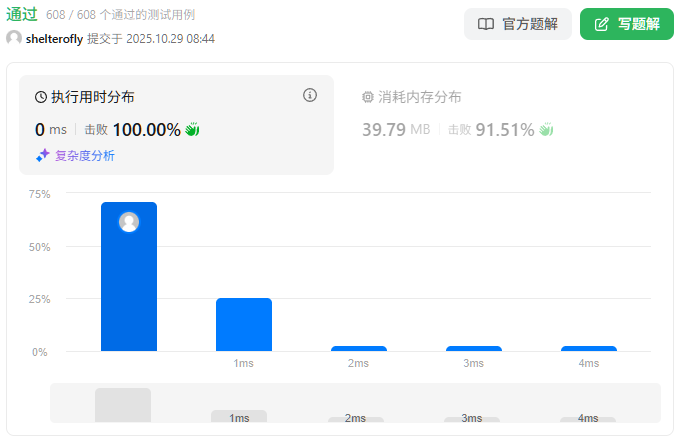
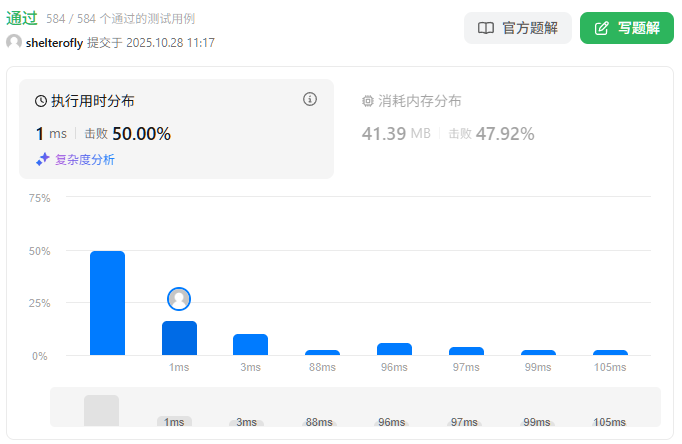
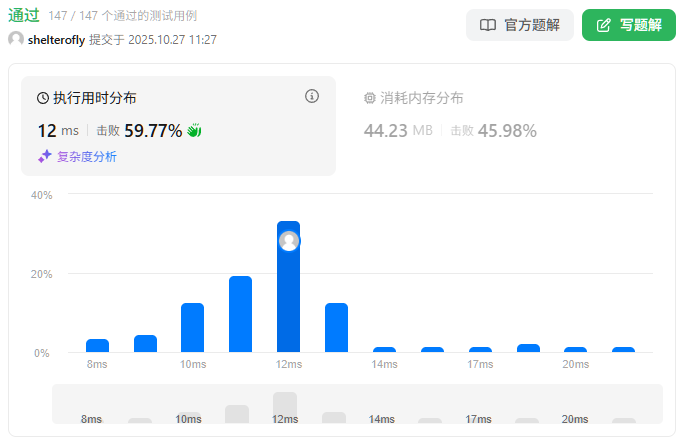
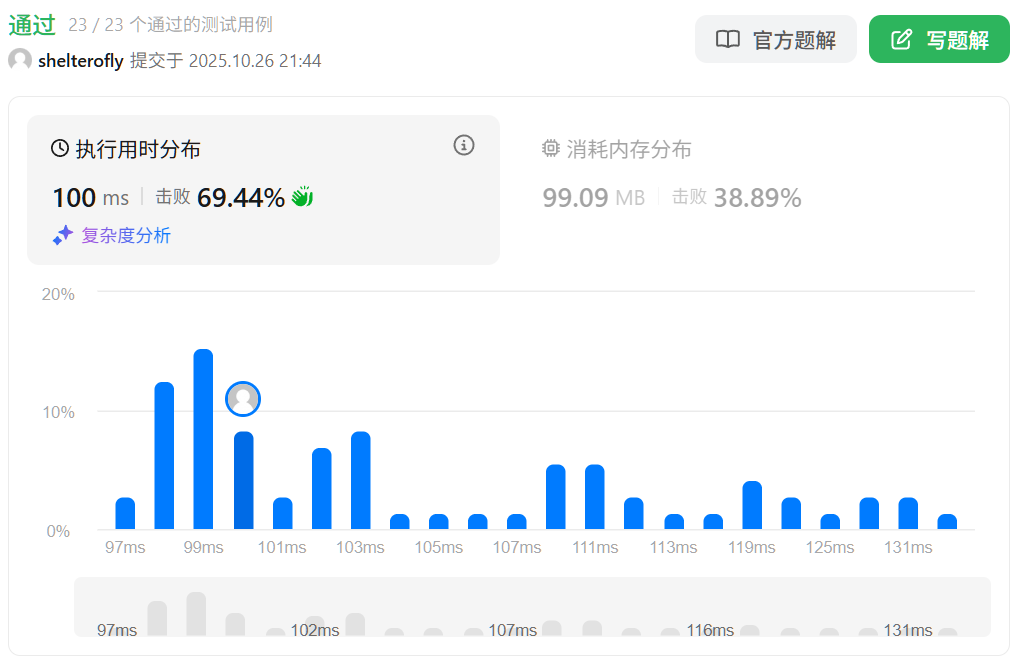
性能