498.对角线遍历

目标

给你一个大小为 m x n 的矩阵 mat ，请以对角线遍历的顺序，用一个数组返回这个矩阵中的所有元素。

示例 1：

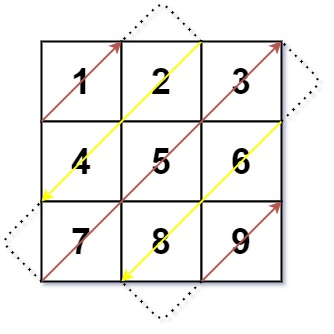
输入：mat = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,4,7,5,3,6,8,9]

示例 2：

输入：mat = [[1,2],[3,4]]
输出：[1,2,3,4]

说明：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 10^4
• 1 <= m * n <= 10^4
• -10^5 <= mat[i][j] <= 10^5

思路

按照左上、右下、左上、右下…… 的顺序枚举矩阵的对角线。

m = 4, n = 3

 1  2   3 (k)
↗ ↙ ↗
↙ ↗ ↙ 4
↗ ↙ ↗ 5
↙ ↗ ↙ 6

(0, 0) (0, 1) (0, 2)
(1, 0) (1, 1) (1, 2)
(2, 0) (2, 1) (2, 2)
(3, 0) (3, 1) (3, 2)

定义 k - 1 = i + j， 可得 j = k - 1 - i

• 当 i = 0 时，j 取得最大值 k - 1，由于 j <= n - 1，因此 maxJ = Math.min(k - 1, n - 1)
• 当 i = m - 1 时，j 取得最小值 k - m，由于 j >= 0，因此 minJ = Math.max(k - m, 0)

代码

/**
 * @date 2025-08-25 8:51
 */
public class FindDiagonalOrder498 {

    public int[] findDiagonalOrder(int[][] mat) {
        int m = mat.length;
        int n = mat[0].length;
        int l = m + n - 1;
        int[] res = new int[m * n];
        int p = 0;
        for (int k = 1; k <= l; k++) {
            int minJ = Math.max(0, k - m);
            int maxJ = Math.min(k - 1, n - 1);
            if (k % 2 == 0) {
                for (int j = maxJ; j >= minJ; j--) {
                    res[p++] = mat[k - 1 - j][j];
                }
            } else {
                for (int j = minJ; j <= maxJ; j++) {
                    res[p++] = mat[k - 1 - j][j];
                }
            }
        }
        return res;
    }

}

性能