月度归档： 2025 年 6 月

目标

和谐数组是指一个数组里元素的最大值和最小值之间的差别 正好是 1 。

给你一个整数数组 nums ，请你在所有可能的 子序列 中找到最长的和谐子序列的长度。

数组的 子序列 是一个由数组派生出来的序列，它可以通过删除一些元素或不删除元素、且不改变其余元素的顺序而得到。

示例 1：

输入：nums = [1,3,2,2,5,2,3,7]
输出：5
解释：
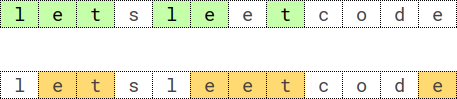
最长和谐子序列是 [3,2,2,2,3]。

示例 2：

输入：nums = [1,2,3,4]
输出：2
解释：
最长和谐子序列是 [1,2]，[2,3] 和 [3,4]，长度都为 2。

示例 3：

输入：nums = [1,1,1,1]
输出：0
解释：
不存在和谐子序列。

说明：

• 1 <= nums.length <= 2 * 10^4
• -10^9 <= nums[i] <= 10^9

思路

统计数字出现次数，求相邻频次之和的最大值。

代码

/**
 * @date 2025-06-30 8:46
 */
public class FindLHS {

    public int findLHS(int[] nums) {
        int n = nums.length;
        Map<Integer, Integer> cnt = new HashMap<>();
        for (int i = 0; i < n; i++) {
            cnt.merge(nums[i], 1, Integer::sum);
        }
        int res = 0;
        for (Map.Entry<Integer, Integer> entry : cnt.entrySet()) {
            int key = entry.getKey();
            Integer nextVal = cnt.get(key + 1);
            if (nextVal != null) {
                res = Math.max(res, entry.getValue() + nextVal);
            }
        }
        return res;
    }
}

性能

目标

给你一个整数数组 nums 和一个整数 k 。你需要找到 nums 中长度为 k 的 子序列 ，且这个子序列的 和最大 。

请你返回 任意 一个长度为 k 的整数子序列。

子序列 定义为从一个数组里删除一些元素后，不改变剩下元素的顺序得到的数组。

示例 1：

输入：nums = [2,1,3,3], k = 2
输出：[3,3]
解释：
子序列有最大和：3 + 3 = 6 。

示例 2：

输入：nums = [-1,-2,3,4], k = 3
输出：[-1,3,4]
解释：
子序列有最大和：-1 + 3 + 4 = 6 。

示例 3：

输入：nums = [3,4,3,3], k = 2
输出：[3,4]
解释：
子序列有最大和：3 + 4 = 7 。
另一个可行的子序列为 [4, 3] 。

说明：

• 1 <= nums.length <= 1000
• -10^5 <= nums[i] <= 10^5
• 1 <= k <= nums.length

思路

返回数组任意一个长度为 k 并且和最大的子序列。

将元素值与下标绑定后按元素值排序，取值最大的 k 个元素，然后再按下标排序即可。

有网友最后没有使用排序，而是记录临界元素 e 以及它在子序列中的个数 cnt，遍历原数组，如果大于 e 直接加入答案，如果等于 e 则需要判断 cnt 的剩余个数。

代码

/**
 * @date 2025-06-28 9:44
 */
public class MaxSubsequence2099 {

    public int[] maxSubsequence(int[] nums, int k) {
        int n = nums.length;
        int[][] arr = new int[n][2];
        for (int i = 0; i < n; i++) {
            arr[i] = new int[]{nums[i], i};
        }
        Arrays.sort(arr, (a, b) -> a[0] - b[0]);
        int[] res = new int[k];
        int[][] subArr = new int[k][2];
        System.arraycopy(arr, n - k, subArr, 0, k);
        Arrays.sort(subArr, (a, b) -> a[1] - b[1]);
        for (int i = 0; i < k; i++) {
            res[i] = subArr[i][0];
        }
        return res;
    }
}

性能

目标

给你一个下标从 0 开始的整数数组 nums 和两个整数 key 和 k 。K 近邻下标 是 nums 中的一个下标 i ，并满足至少存在一个下标 j 使得 |i - j| <= k 且 nums[j] == key 。

以列表形式返回按 递增顺序 排序的所有 K 近邻下标。

示例 1：

输入：nums = [3,4,9,1,3,9,5], key = 9, k = 1
输出：[1,2,3,4,5,6]
解释：因此，nums[2] == key 且 nums[5] == key 。
- 对下标 0 ，|0 - 2| > k 且 |0 - 5| > k ，所以不存在 j 使得 |0 - j| <= k 且 nums[j] == key 。所以 0 不是一个 K 近邻下标。
- 对下标 1 ，|1 - 2| <= k 且 nums[2] == key ，所以 1 是一个 K 近邻下标。
- 对下标 2 ，|2 - 2| <= k 且 nums[2] == key ，所以 2 是一个 K 近邻下标。
- 对下标 3 ，|3 - 2| <= k 且 nums[2] == key ，所以 3 是一个 K 近邻下标。
- 对下标 4 ，|4 - 5| <= k 且 nums[5] == key ，所以 4 是一个 K 近邻下标。
- 对下标 5 ，|5 - 5| <= k 且 nums[5] == key ，所以 5 是一个 K 近邻下标。
- 对下标 6 ，|6 - 5| <= k 且 nums[5] == key ，所以 6 是一个 K 近邻下标。
因此，按递增顺序返回 [1,2,3,4,5,6] 。 

示例 2：

输入：nums = [2,2,2,2,2], key = 2, k = 2
输出：[0,1,2,3,4]
解释：对 nums 的所有下标 i ，总存在某个下标 j 使得 |i - j| <= k 且 nums[j] == key ，所以每个下标都是一个 K 近邻下标。 
因此，返回 [0,1,2,3,4] 。

说明：

• 1 <= nums.length <= 1000
• 1 <= nums[i] <= 1000
• key 是数组 nums 中的一个整数
• 1 <= k <= nums.length

思路

返回数组中元素值为 key 的 k 临近下标，即元素 key 的下标以及其左右 k 个下标。要求以递增顺序返回，不能包含重复下标。

遍历数组，判断 nums[i] 是否等于 k，如果相等则将左右两侧的 k 个下标加入答案。使用一个指针标记当前已经记录的最大下标，避免将重复的下标加入答案。

代码

/**
 * @date 2025-06-24 0:11
 */
public class FindKDistantIndices2200 {

    public List<Integer> findKDistantIndices(int[] nums, int key, int k) {
        List<Integer> res = new ArrayList<>();
        int n = nums.length;
        int r = -1;
        for (int i = 0; i < n; i++) {
            if (nums[i] == key) {
                int l = Math.max(r + 1, i - k);
                r = Math.min(n - 1, i + k);
                for (int j = l; j <= r; j++) {
                    res.add(j);
                }
            }
        }
        return res;
    }

}

性能

目标

字符串 s 可以按下述步骤划分为若干长度为 k 的组：

• 第一组由字符串中的前 k 个字符组成，第二组由接下来的 k 个字符串组成，依此类推。每个字符都能够成为 某一个 组的一部分。
• 对于最后一组，如果字符串剩下的字符 不足 k 个，需使用字符 fill 来补全这一组字符。

注意，在去除最后一个组的填充字符 fill（如果存在的话）并按顺序连接所有的组后，所得到的字符串应该是 s 。

给你一个字符串 s ，以及每组的长度 k 和一个用于填充的字符 fill ，按上述步骤处理之后，返回一个字符串数组，该数组表示 s 分组后 每个组的组成情况。

示例 1：

输入：s = "abcdefghi", k = 3, fill = "x"
输出：["abc","def","ghi"]
解释：
前 3 个字符是 "abc" ，形成第一组。
接下来 3 个字符是 "def" ，形成第二组。
最后 3 个字符是 "ghi" ，形成第三组。
由于所有组都可以由字符串中的字符完全填充，所以不需要使用填充字符。
因此，形成 3 组，分别是 "abc"、"def" 和 "ghi" 。

示例 2：

输入：s = "abcdefghij", k = 3, fill = "x"
输出：["abc","def","ghi","jxx"]
解释：
与前一个例子类似，形成前三组 "abc"、"def" 和 "ghi" 。
对于最后一组，字符串中仅剩下字符 'j' 可以用。为了补全这一组，使用填充字符 'x' 两次。
因此，形成 4 组，分别是 "abc"、"def"、"ghi" 和 "jxx" 。

说明：

• 1 <= s.length <= 100
• s 仅由小写英文字母组成
• 1 <= k <= 100
• fill 是一个小写英文字母

思路

将字符串划分为长度为 k 的组，如果长度不足则使用 fill 补全。

代码

/**
 * @date 2025-06-22 12:16
 */
public class DivideString2138 {

    public String[] divideString(String s, int k, char fill) {
        int n = s.length();
        String[] res = new String[n / k + (n % k == 0 ? 0 : 1)];
        char[] chars = s.toCharArray();
        StringBuilder sb = new StringBuilder();
        int j = 0;
        for (int i = 0; i < n; i++) {
            if (i != 0 && i % k == 0) {
                res[j++] = sb.toString();
                sb = new StringBuilder();
            }
            sb.append(chars[i]);
        }
        int cnt = k - sb.length();
        while (cnt > 0) {
            sb.append(fill);
            cnt--;
        }
        if (j == res.length - 1) {
            res[j] = sb.toString();
        }
        return res;
    }

}

性能